Question

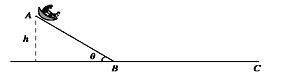
【题目】如图所示，质量M=2kg、长s1=15m的木板A静止在光滑水平面上，其右端上表面紧靠着一固定斜面的底端，斜面倾角θ=37°，质量m=0.5kg的木块B从斜面上距斜面底端s2=8m处由静止释放，经过斜面底端滑到木板上，从斜面底端滑上木板时速度大小不变。木块B可视作质点，与木板A上表面间的动摩擦因数为μ1＝0.2，与斜面间的动摩擦因数μ2＝0.25。若取sinθ=0.6，cosθ=0.8，g =10 m/s2。求：

(1)木块B刚滑上木板A时的速度有多大？

(2)木块B最终会不会离开木板？如果会，请计算木块在木板上滑动的时间；如果不会，请计算木块停在木板上的位置距木板左端多远。

Answer 1

【答案】(1)8m/s;(2)2.2m

【解析】

（1）根据牛顿第二定律求解木块B在斜面上滑动过程中的加速度，根据速度位移公式求解木块B刚滑上木板A时的速度；（2）根据牛顿第二定律求解滑块和木板的加速度，根据运动公式求解木板和木块的位移，求解位移之差可判断木块B最终会不会离开木板.

（1）设木块B在斜面上滑动过程中的加速度是a，木块B刚滑上木板A时的速度是v1，则

mgsinθ－μ2mgcosθ＝ma

解得：v1＝8m/s

（2）假设木块B最终没有离开木板。设在木板上滑行的时间是t，木块B与木板最后共同速度是v2，木块B在木板上滑行的过程中，木块的加速度大小是a1，通过的距离是L1，木板的加速度大小是a1，通过的距离是L2，则

μ1mg＝ma1

μ1mg＝Ma2

a1＝2m/s2，a2＝0.5m/s2

v2＝a2t

v2＝v1－a1t

解得：v2＝1.6m/s,t＝3.2s，L1＝15.36m，L2＝2.56m

L1－L2=12.80m＜s1=15m,所以木块B最终没有离开木板；

设木块停在木板上的位置距木板左端距离是x，则x＝L2＋s1－L1＝2.2m