题目内容
【题目】在海滨游乐场有一种滑沙的娱乐活动.如图所示,人坐在滑板上从斜坡的高处A点由静止开始下滑,滑到斜坡底部B点后沿水平滑道再滑行一段距离到C点停下来,斜坡滑道与水平滑道间是平滑连接的,滑板与两滑道间的动摩擦因数均为μ=0.5, 不计空气阻力, 重力加速度g=10m/s2, 斜坡倾角θ=37°.(sin37°=0.6,cos37°=0.8)
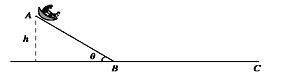
(1)若人和滑板的总质量为m=60kg,求人在斜坡上下滑时的加速度大小.
(2)若由于受到场地的限制,A点到C点的水平距离为S= 50m,为确保人身安全,假如你是设计师,你认为在设计斜坡滑道时,对高度h应有怎样的要求?
【答案】
【1】 2m/s2
【2】 h=25m
【解析】
(1)对人与滑板应用牛顿第二定律可以求出加速度.
(2)人在斜面上做加速运动,到达水平面上之后做匀减速运动,确保安全,人滑到C点前的速度必须为0,由动能定理可得可求得最大高度.
(1)对人和滑板,由牛顿第二定律得:mgsinθ-μmgcosθ=ma1,
解得:a1=g(sinθ-μcosθ)=10(0.6-0.5×0.8)=2m/s2 ,
(2)斜坡倾角为α,最大高度为h,
则斜面长sAB=![]() ,水平面BC长sBC=s-sABcosθ=s-
,水平面BC长sBC=s-sABcosθ=s-![]() ,
,
为确保安全,人滑到C点前的速度必须为0,
由动能定理可得:mgh-(μNsAB+μmgsBC)=0,
即mgh-μmgcosα![]() -μmg(s-
-μmg(s-![]() )=mgh-μmgs=0,
)=mgh-μmgs=0,
代入数据解得:h=25m.
本题是对牛顿第二定律的应用,对物体受力分析可以求得加速度的大小,再利用动能定理可以求得高度的大小.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目