题目内容
19.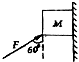 木块M的重量是60N,用于竖直方向成60°角的大小为100N的力F作用于木块时,木块静止于墙上,如图所示,此时作用于木块的摩擦力的大小为10N,方向向下,当F为120N时,墙壁对木块恰好没有摩擦力,此时木块对墙壁的正压力为$60\sqrt{3}N$.
木块M的重量是60N,用于竖直方向成60°角的大小为100N的力F作用于木块时,木块静止于墙上,如图所示,此时作用于木块的摩擦力的大小为10N,方向向下,当F为120N时,墙壁对木块恰好没有摩擦力,此时木块对墙壁的正压力为$60\sqrt{3}N$.
分析 对木块受力分析,并将力进行分解,根据受力平衡条件,结合竖直方向的分力与重力的大小关系来确定摩擦力方向及大小.
解答  解:假设摩擦力的方向向上,对木块受力分析,如图所示,
解:假设摩擦力的方向向上,对木块受力分析,如图所示,
根据力的平行四边形定则,将力F进行水平与竖直方向分解,即为F1=Fsinθ,而F2=Fcosθ;
根据平衡条件可知,此时作用于木块的摩擦力的大小为f=F2-G=$100×\frac{1}{2}-60=-10N$,负号表示摩擦力方向向下,
当摩擦力为零时,Fcosθ=60N,解得:F=120N,此时木块对墙壁的正压力为:F1=Fsinθ=120×$\frac{\sqrt{3}}{2}$=$60\sqrt{3}N$.
故答案为:10N,向下,120,$60\sqrt{3}N$
点评 考查受力分析与力的处理法则,掌握平衡状态方程,注意竖直的分力与重力大小比较是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.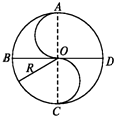 一人晨练,按图所示走半径为R的中国古代八卦图,中央S部分是两个直径为R的半圆,BD、CA分别为西东、南北指向.他从A点出发沿曲线ABCOADC行进,则当他到D点时,他的路程和位移大小及位移的方向分别为( )
一人晨练,按图所示走半径为R的中国古代八卦图,中央S部分是两个直径为R的半圆,BD、CA分别为西东、南北指向.他从A点出发沿曲线ABCOADC行进,则当他到D点时,他的路程和位移大小及位移的方向分别为( )
 一人晨练,按图所示走半径为R的中国古代八卦图,中央S部分是两个直径为R的半圆,BD、CA分别为西东、南北指向.他从A点出发沿曲线ABCOADC行进,则当他到D点时,他的路程和位移大小及位移的方向分别为( )
一人晨练,按图所示走半径为R的中国古代八卦图,中央S部分是两个直径为R的半圆,BD、CA分别为西东、南北指向.他从A点出发沿曲线ABCOADC行进,则当他到D点时,他的路程和位移大小及位移的方向分别为( )| A. | 2πR R 向西南 | B. | 2.5πR $\sqrt{2}$R 向东南 | C. | πR R 向东南 | D. | 3πR R 向西北 |
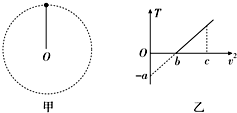
4.如图甲所示,用一轻质绳拴着一质量为m的小球,在竖直平面内做圆周运动(不计一切阻力),小球运动到最高点时绳对小球的拉力为T,小球在最高点的速度大小为v,其T--v2图象如图乙所示,则( )

| A. | 轻质绳长为$\frac{am}{b}$ | |
| B. | 当地的重力加速度为$\frac{a}{m}$ | |
| C. | 当v2=c时,轻质绳的拉力大小为$\frac{ac}{b}$+a | |
| D. | 只要v2≥b,小球在最低点和最高点时绳的拉力差均为6a |
11.一个质量为m的物体以a=2g的加速度竖直向上加速运动,则在此物体上升h的过程中,下列说法正确的是( )
| A. | 物体的重力势能增加了2mgh | B. | 物体的动能增加了2mgh | ||
| C. | 物体的机械能保持不变 | D. | 物体的机械能增加了3mgh |

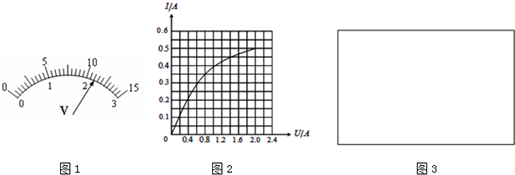
 如图所示,光滑小球静止在两个平面间,一个面恰水平,一个面倾斜,则小球受到的作用力有2个,它们分别是重力和水平面的支持力.
如图所示,光滑小球静止在两个平面间,一个面恰水平,一个面倾斜,则小球受到的作用力有2个,它们分别是重力和水平面的支持力.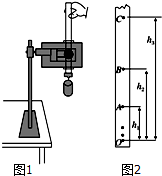 利用如图所示的装置验证机械能守恒定律.
利用如图所示的装置验证机械能守恒定律.