题目内容
5.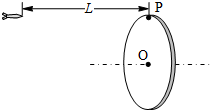 如图所示,一位同学玩飞镖游戏.圆盘最上端有一P点,飞镖抛出时与P等高,且距离P点为L.当飞镖以初速度v0垂直盘面瞄准P点抛出的同时,圆盘以经过盘心O点的水平轴在竖直平面内匀速转动.忽略空气阻力,重力加速度为g,若飞镖恰好击中P点,则( )
如图所示,一位同学玩飞镖游戏.圆盘最上端有一P点,飞镖抛出时与P等高,且距离P点为L.当飞镖以初速度v0垂直盘面瞄准P点抛出的同时,圆盘以经过盘心O点的水平轴在竖直平面内匀速转动.忽略空气阻力,重力加速度为g,若飞镖恰好击中P点,则( )| A. | 飞镖击中P点所需的时间为$\frac{L}{{{{v}_0}}}$ | |
| B. | 圆盘的半径可能为$\frac{{g{L^2}}}{{2{v}_0^2}}$ | |
| C. | 圆盘转动角速度的最小值为$\frac{2π{v}_{0}}{L}$ | |
| D. | P点随圆盘转动的线速度可能为$\frac{5πgL}{4{v}_{0}}$ |
分析 飞镖做平抛运动的同时,圆盘上P点做匀速圆周运动,恰好击中P点,说明A点正好在最低点被击中,则P点转动的时间t=(2n+1)$•\frac{T}{2}$,根据平抛运动水平位移可求得平抛的时间,两时间相等联立可求解.
解答 解:A、飞镖水平抛出做平抛运动,在水平方向做匀速直线运动,因此t=$\frac{L}{{v}_{0}}$,故A正确.
B、飞镖击中P点时,P恰好在最下方,则2r=$\frac{1}{2}g{t}^{2}$,解得圆盘的半径 r=$\frac{g{L}^{2}}{4{v}_{0}^{2}}$,故B错误.
C、飞镖击中P点,则P点转过的角度满足 θ=ωt=π+2kπ(k=0,1,2…)
故ω=$\frac{θ}{t}$=$\frac{(2k+1)π{v}_{0}}{L}$,则圆盘转动角速度的最小值为 $\frac{π{v}_{0}}{L}$.故C错误.
D、P点随圆盘转动的线速度为 v=ωr=$\frac{(2k+1)π{v}_{0}}{L}$•$\frac{g{L}^{2}}{4{v}_{0}^{2}}$=$\frac{(2k+1)πgL}{4{v}_{0}}$
当k=2时,v=$\frac{5πgL}{4{v}_{0}}$.故D正确.
故选:AD.
点评 本题关键知道恰好击中P点,说明P点正好在最低点,利用匀速圆周运动的周期性和平抛运动规律联立求解.

练习册系列答案
相关题目
16. 用一根横截面积为S、电阻率为ρ的硬质导线做成一个半径为r的圆环,ab为圆环的直径.如图所示,在ab的左侧存在一个匀强磁场,磁场垂直圆环所在平面,方向如图,磁感应强度大小随时间的变化率$\frac{△B}{△t}$=k(k<0),则( )
用一根横截面积为S、电阻率为ρ的硬质导线做成一个半径为r的圆环,ab为圆环的直径.如图所示,在ab的左侧存在一个匀强磁场,磁场垂直圆环所在平面,方向如图,磁感应强度大小随时间的变化率$\frac{△B}{△t}$=k(k<0),则( )
 用一根横截面积为S、电阻率为ρ的硬质导线做成一个半径为r的圆环,ab为圆环的直径.如图所示,在ab的左侧存在一个匀强磁场,磁场垂直圆环所在平面,方向如图,磁感应强度大小随时间的变化率$\frac{△B}{△t}$=k(k<0),则( )
用一根横截面积为S、电阻率为ρ的硬质导线做成一个半径为r的圆环,ab为圆环的直径.如图所示,在ab的左侧存在一个匀强磁场,磁场垂直圆环所在平面,方向如图,磁感应强度大小随时间的变化率$\frac{△B}{△t}$=k(k<0),则( )| A. | 圆环具有扩张的趋势 | |
| B. | 圆环中产生逆时针方向的感应电流 | |
| C. | 圆环中感应电流的大小为$\frac{krS}{2ρ}$ | |
| D. | 图中a、b两点之间的电势差UAB=|$\frac{1}{4}$kπr2| |
20.一物体在四个共点力作用下做匀速直线运动.若突然撤去一个沿运动方向的力,其余三个力保持不变,则物体做( )
| A. | 匀速圆周运动 | B. | 匀加速直线运动 | C. | 类平抛运动 | D. | 匀减速直线运动 |
17. 如图所示,倾角为θ的斜面体c置于水平地面上,小物块b置于斜面上,通过绝缘细绳跨过光滑的定滑轮与带正电小球M连接,连接b的一段细绳与斜面平行,带负电的小球N固定在M的正下方.两带电小球在缓慢漏电的过程中,M、b、c都处于静止状态,下列说法中正确的是( )
如图所示,倾角为θ的斜面体c置于水平地面上,小物块b置于斜面上,通过绝缘细绳跨过光滑的定滑轮与带正电小球M连接,连接b的一段细绳与斜面平行,带负电的小球N固定在M的正下方.两带电小球在缓慢漏电的过程中,M、b、c都处于静止状态,下列说法中正确的是( )
 如图所示,倾角为θ的斜面体c置于水平地面上,小物块b置于斜面上,通过绝缘细绳跨过光滑的定滑轮与带正电小球M连接,连接b的一段细绳与斜面平行,带负电的小球N固定在M的正下方.两带电小球在缓慢漏电的过程中,M、b、c都处于静止状态,下列说法中正确的是( )
如图所示,倾角为θ的斜面体c置于水平地面上,小物块b置于斜面上,通过绝缘细绳跨过光滑的定滑轮与带正电小球M连接,连接b的一段细绳与斜面平行,带负电的小球N固定在M的正下方.两带电小球在缓慢漏电的过程中,M、b、c都处于静止状态,下列说法中正确的是( )| A. | b对c的摩擦力可能始终增加 | B. | 地面对c的支撑力始终变小 | ||
| C. | c对地面的摩擦力方向始终向左 | D. | 滑轮对绳的作用力方向始终不变 |

 固定有竖直杆的小车总质量为M,在竖直杆上套一个质量为m的球,已知球与竖直杆之间的动摩擦因数为μ,要使球能沿杆匀速下滑,则对小车施加的水平作用力F=$\frac{1}{μ}$(M+m)g,此时小车的加速度a=$\frac{g}{μ}$(不计地面的摩擦).
固定有竖直杆的小车总质量为M,在竖直杆上套一个质量为m的球,已知球与竖直杆之间的动摩擦因数为μ,要使球能沿杆匀速下滑,则对小车施加的水平作用力F=$\frac{1}{μ}$(M+m)g,此时小车的加速度a=$\frac{g}{μ}$(不计地面的摩擦).
 如图所示,质量为m、边长为L的正方形线圈ABCD由n匝导线绕成,导线中通有顺时针方向大小为I的电流,在AB边的中点用细线竖直悬挂于轻杆右端,轻杆左端通过竖直的弹簧与地面相连,轻杆可绕杆中央的固定转轴O在竖直平面内转动.在图中虚线的下方,有与线圈平面垂直的匀强磁场,磁感强度为B,平衡时,CD边水平且线圈有一半面积在磁场中,忽略电流I产生的磁场,穿过线圈的磁通量为$\frac{B{L}^{2}}{2}$;弹簧受到的拉力为mg+nBIL.
如图所示,质量为m、边长为L的正方形线圈ABCD由n匝导线绕成,导线中通有顺时针方向大小为I的电流,在AB边的中点用细线竖直悬挂于轻杆右端,轻杆左端通过竖直的弹簧与地面相连,轻杆可绕杆中央的固定转轴O在竖直平面内转动.在图中虚线的下方,有与线圈平面垂直的匀强磁场,磁感强度为B,平衡时,CD边水平且线圈有一半面积在磁场中,忽略电流I产生的磁场,穿过线圈的磁通量为$\frac{B{L}^{2}}{2}$;弹簧受到的拉力为mg+nBIL. 如图所示,AB为半径R=0.8m的$\frac{1}{4}$光滑圆弧轨道,下端B恰与平板小车右端平滑对接.小车质量M=3kg,车长L=2.06m.现有一质量m=1kg的小滑块,由轨道顶端无初速释放,滑到B端后冲上小车.已知地面光滑,滑块与小车上表面间的动摩擦因数μ=0.3,当车运行了1.5s时,车被地面装置锁定.(g=10m/s2)试求:
如图所示,AB为半径R=0.8m的$\frac{1}{4}$光滑圆弧轨道,下端B恰与平板小车右端平滑对接.小车质量M=3kg,车长L=2.06m.现有一质量m=1kg的小滑块,由轨道顶端无初速释放,滑到B端后冲上小车.已知地面光滑,滑块与小车上表面间的动摩擦因数μ=0.3,当车运行了1.5s时,车被地面装置锁定.(g=10m/s2)试求: