题目内容
半径为a的圆形区域内有均匀磁场,磁感应强度为B=0.2 T,磁场方向垂直纸面向里,半径为b的金属圆环与磁场同心地放置,磁场与环面垂直,其中a=(1)若棒以v0=

图
(2)撤去中间的金属棒MN,将右面的半圆环OL2O′以OO′为轴向上翻转90°,若此时磁场随时间均匀变化,其变化率为![]() T/s,求L1的功率.
T/s,求L1的功率.
解析:(1)棒滑过圆环直径时切割磁感线的有效长度L=
E=BLv=0.2×2×0.4×5 V=0.8 V
当不计棒与环的电阻时,直径OO′两端的电压U=E=0.8 V,所以通过灯L1的电流为
I1=![]() =
=
(2)右半圆环向上翻转90°后,穿过回路的磁场有效面积变为原来的一半,即S′=![]() πa2.磁场变化时在回路中产生的感应电动势为
πa2.磁场变化时在回路中产生的感应电动势为
E′=![]() =2×(0.4)2 V=0.32 V
=2×(0.4)2 V=0.32 V
由于L1、L2两灯相同,圆环电阻不计,所以每灯的电压均为
U′=![]() E′,L1的功率为
E′,L1的功率为
P1= W=1.28×10-2 W
W=1.28×10-2 W
答案:(1)0.8 V,

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
 半径为a的圆形区域内有均匀磁场,磁感强度为B=0.3T,磁场方向垂直纸面向里,半径为b的金属圆环与磁场同心放置,磁场与环面垂直,其中a=0.2m,b=0.4m,金属环上分别接有灯L1、L2,两灯的电阻均为R=1Ω,一金属棒MN与金属环接触良好,棒单位长度的电阻R0=0.5Ω/m,金属环的电阻忽略不计.求:
半径为a的圆形区域内有均匀磁场,磁感强度为B=0.3T,磁场方向垂直纸面向里,半径为b的金属圆环与磁场同心放置,磁场与环面垂直,其中a=0.2m,b=0.4m,金属环上分别接有灯L1、L2,两灯的电阻均为R=1Ω,一金属棒MN与金属环接触良好,棒单位长度的电阻R0=0.5Ω/m,金属环的电阻忽略不计.求: (2001?上海)半径为a的圆形区域内有均匀磁场,磁感应强度为B=0.2T,磁场方向垂直纸面向里,半径为b的金属圆环与磁场同心地放置,磁场与环面垂直,其中a=0.4m,b=0.6m.金属环上分别接有灯L1、L2,两灯的电阻均为R=2Ω,一金属棒MN与金属环接触良好,棒与环的电阻均忽略不计.
(2001?上海)半径为a的圆形区域内有均匀磁场,磁感应强度为B=0.2T,磁场方向垂直纸面向里,半径为b的金属圆环与磁场同心地放置,磁场与环面垂直,其中a=0.4m,b=0.6m.金属环上分别接有灯L1、L2,两灯的电阻均为R=2Ω,一金属棒MN与金属环接触良好,棒与环的电阻均忽略不计. 如图所示,空间存在垂直于纸面的均匀磁场,在半径为a的圆形区域内、外,磁场方向相反,磁感应强度的大小均为B.一半径为b,电阻为R的圆形导线环放置在纸面内,其圆心与圆形区域的中心重合.在内、外磁场同时由B均匀地减小到零的过程中,通过导线截面的电量Q=
如图所示,空间存在垂直于纸面的均匀磁场,在半径为a的圆形区域内、外,磁场方向相反,磁感应强度的大小均为B.一半径为b,电阻为R的圆形导线环放置在纸面内,其圆心与圆形区域的中心重合.在内、外磁场同时由B均匀地减小到零的过程中,通过导线截面的电量Q= 在半径为a的圆形区域内有垂直纸面向里的匀强磁场,如图所示,两个电子从P孔沿半径PO方向射入磁场后,分别从A、C孔射出,已知圆心角∠POA=90°、∠POC=120°.则从AC射出的电子速度大小vA:vC=
在半径为a的圆形区域内有垂直纸面向里的匀强磁场,如图所示,两个电子从P孔沿半径PO方向射入磁场后,分别从A、C孔射出,已知圆心角∠POA=90°、∠POC=120°.则从AC射出的电子速度大小vA:vC=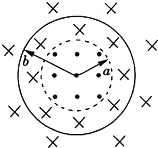 在一空间有方向相反,磁感应强度大小均为B的匀强磁场,如图所示,向外的磁场分布在一半径为a的圆形区域内,向内的磁场分布在除圆形区域外的整个区域,该平面内有一半径为b(b>
在一空间有方向相反,磁感应强度大小均为B的匀强磁场,如图所示,向外的磁场分布在一半径为a的圆形区域内,向内的磁场分布在除圆形区域外的整个区域,该平面内有一半径为b(b>