题目内容
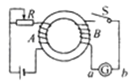
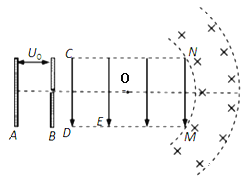
【题目】如图所示,竖直放置的平行金属板A、B间电压为U0,在B板右侧CDMN矩形区域存在竖直向下的匀强电场,DM边长为L,CD边长为![]() L,紧靠电场右边界存在垂直纸面水平向里的有界匀强磁场,磁场左右边界为同心圆,圆心O在CDMN矩形区域的几何中心,磁场左边界刚好过M、N两点。质量为m、电荷量为+q的带电粒子,从A板由静止开始经A、B极板间电场加速后,从边界CD中点水平向右进入矩形区域的匀强电场,飞出电场后进入匀强磁场。当矩形区域中的场强取某一值时,粒子从M点进入磁场,经磁场偏转后从N点返回电场区域,且粒子在磁场中运动轨迹恰与磁场右边界相切,粒子的重力忽略不计,sin37°=0.6,cos37°=0.8。
L,紧靠电场右边界存在垂直纸面水平向里的有界匀强磁场,磁场左右边界为同心圆,圆心O在CDMN矩形区域的几何中心,磁场左边界刚好过M、N两点。质量为m、电荷量为+q的带电粒子,从A板由静止开始经A、B极板间电场加速后,从边界CD中点水平向右进入矩形区域的匀强电场,飞出电场后进入匀强磁场。当矩形区域中的场强取某一值时,粒子从M点进入磁场,经磁场偏转后从N点返回电场区域,且粒子在磁场中运动轨迹恰与磁场右边界相切,粒子的重力忽略不计,sin37°=0.6,cos37°=0.8。
(1)求粒子离开B板时的速度v1;
(2)求磁场右边界圆周的半径R;
(3)将磁感应强度大小和矩形区域的场强大小改变为适当值时,粒子从MN间飞入磁场,经磁场偏转返回电场前,在磁场中运动的时间有最大值,求此最长时间tm。
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;
;
【解析】
(1)粒子从A到B的加速过程中,由动能定理有:![]()
解得:![]() ;
;
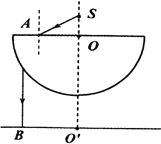
(2)如图1所示,
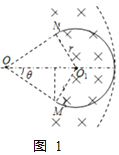
粒子刚好沿着磁场右边界到达N点,图中![]() ,θ=37°,
,θ=37°,
带电粒子在磁场中做圆周运动的半径为:![]()
则磁场区域的半径:![]() ;
;
(3)粒子从同一点离开电场时,在磁场中运动轨迹与右边界相切时弧长最长,运动时间也最长;
粒子从不同点离开电场,在磁场中运动轨迹与右边界相切时弧长最长,且当矩形区域场强为零时,粒子进入磁场时速度最小,粒子在磁场中运动时间最长,
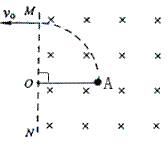
则画出粒子运动轨迹如图2所示,
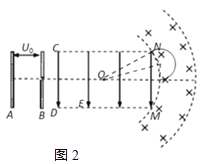
由几何关系知粒子偏转360°-2(90°-37°0)=254°,
则最长时间为:![]() ;
;

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案【题目】在做“研究匀变速直线运动”的实验时,某同学得到一条用电火花计时器打下的纸带如图所示,并在其上取了A、B、C、D、E、F、G7个计数点,每相邻两个计数点间还有4个点图中没有画出,电火花计时器接220V、50Hz交流电源.
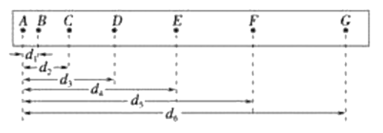
(1)设电火花计时器的周期为T,计算F点的瞬时速度vF的公式为vF=__________;
(2)他经过测量并计算得到电火花计时器在打B、C、D、E、F各点时物体的瞬时速度如下表.以A点对应的时刻为t=0,试在下图所示坐标系中合理地选择标度,作出v--t图象______,并利用该图象求出物体的加速度a=_________(保留两位有效数字)
对应点 | B | C | D | E | F |
速度(m/s) | 0.141 | 0.180 | 0.218 | 0.262 | 0.301 |
(3)如果当时电网中交变电流的电压变成210V,而做实验的同学并不知道,那么加速度的测量值与实际值相比______________.(填“偏大”、“偏小”或“不变”)