题目内容
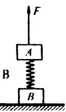
如图所示,质量分别为m1和m2的两物块放在水平地面上,与水平面间的动摩擦因数都为μ(μ≠0),用轻弹簧将两物块连接在一起。当用水平力F作用在m1上时,两物块均以加速度a做匀加速运动,此时,弹簧伸长量为x ;若用水平力F’仍作用在m1上,两物块均以加速度a’=2a做匀加速运动,此时,弹簧伸长量为x’。则下列关系正确的是:( )

A、F’=2F B、x’=2x
C、F’>2F B、x’<2x

A、F’=2F B、x’=2x
C、F’>2F B、x’<2x
D
考点:
分析:本题可先对整体用牛顿第二定律列式求出加速度,再隔离出m2用牛顿第二定律列式求出弹簧弹力.
解答:解:拉力为F时,对两个物体整体,由牛顿第二定律得:
F-μ(m1+m2)g=(m1+m2)a ①;
假设弹簧弹力为F1,对质量为m2的物体,有:
F1-μm2g=m2a ②;
拉力为F’时,a’=2a,对两个物体整体而言,由牛顿第二定律得:
F’-μ(m1+m2)g=(m1+m2)2a ③;
假设弹簧弹力为F1′,对质量为m2的物体,有:
F1′-μm2g=2m2a′④;
由①③两式可解得:F’<2F ⑤;故AC错误;
由②④⑤三式可解得,F1′<2F1;
由胡克定律公式得,F1=kx,F1′=kx′,因而有x′<2x,故B错误,D正确.
故选D.
点评:本题关键为拉力变为2倍,合力变得大于2倍;弹簧弹力与地面是否粗糙无关!
分析:本题可先对整体用牛顿第二定律列式求出加速度,再隔离出m2用牛顿第二定律列式求出弹簧弹力.
解答:解:拉力为F时,对两个物体整体,由牛顿第二定律得:
F-μ(m1+m2)g=(m1+m2)a ①;
假设弹簧弹力为F1,对质量为m2的物体,有:
F1-μm2g=m2a ②;
拉力为F’时,a’=2a,对两个物体整体而言,由牛顿第二定律得:
F’-μ(m1+m2)g=(m1+m2)2a ③;
假设弹簧弹力为F1′,对质量为m2的物体,有:
F1′-μm2g=2m2a′④;
由①③两式可解得:F’<2F ⑤;故AC错误;
由②④⑤三式可解得,F1′<2F1;
由胡克定律公式得,F1=kx,F1′=kx′,因而有x′<2x,故B错误,D正确.
故选D.
点评:本题关键为拉力变为2倍,合力变得大于2倍;弹簧弹力与地面是否粗糙无关!

练习册系列答案
相关题目
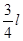 时将物块由静止开始释放,且物块在以后的运动中,斜面体始终处于静止状态。重力加速度为
时将物块由静止开始释放,且物块在以后的运动中,斜面体始终处于静止状态。重力加速度为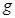 。
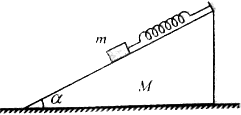
。
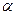 多大?
多大?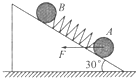

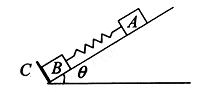
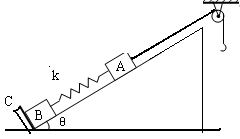
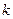 ,C为一固定挡板。系统处于静止状态。现给物块A一初速度使之沿斜面向上运动,当A运动至最高点时,B恰好不离开C,试求A向上运动的最大位移及此时A的加速度。
,C为一固定挡板。系统处于静止状态。现给物块A一初速度使之沿斜面向上运动,当A运动至最高点时,B恰好不离开C,试求A向上运动的最大位移及此时A的加速度。