题目内容
5. 如图所示,在水平面固定一倾角θ=30°的光滑斜面(水平面与斜面用一小段圆弧相连),一光滑木块甲从斜面上高h=5cm的A点由静止释放,同时一木块乙在水平面的C点已初速度v0向右运动,经过时间t=1s,两木块在水平面上相碰.已知C点到斜面底端B的距离L=3.8m,木块乙与水平面间的动摩擦因数μ=0.2,取g=10m/s2,求木块乙的初速度v0.
如图所示,在水平面固定一倾角θ=30°的光滑斜面(水平面与斜面用一小段圆弧相连),一光滑木块甲从斜面上高h=5cm的A点由静止释放,同时一木块乙在水平面的C点已初速度v0向右运动,经过时间t=1s,两木块在水平面上相碰.已知C点到斜面底端B的距离L=3.8m,木块乙与水平面间的动摩擦因数μ=0.2,取g=10m/s2,求木块乙的初速度v0.
分析 根据牛顿第二定律求出甲球在斜面上的加速度,通过位移时间公式求出在斜面上的运动时间以及到达底端的速度,结合两球的位移关系,求出乙的速度.
解答 解:对甲,由牛顿第二定律得:a=$\frac{mgsin30°}{m}$=5m/s2,
由位移公式得:$\frac{h}{sinθ}$=$\frac{1}{2}$at12,
解得:t1=0.2s,
v1=at1=1m/s,
由题意可知:v0(t-t1)-$\frac{1}{2}$μg(t-t1)2+v1(t-t1)=L
代入数据解得:v0=4m/s;
答:木块乙的初速度v0是4m/s.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,知道加速度是联系力学和运动学的桥梁,对于追及问题,关键抓住位移关系和时间关系,运用运动学公式进行求解.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
16. 压敏电阻的阻值随所受压力的增大而减小,右位同学利用压敏电阻设计了判断小车运动状态的装置,其工作原理如图(a)所示,将压敏电阻和一块挡板固定在绝缘小车上,中间放置一个绝缘重球.小车向右做直线运动过程中,电流表示数如图(b)所示,下列判断正确的是( )
压敏电阻的阻值随所受压力的增大而减小,右位同学利用压敏电阻设计了判断小车运动状态的装置,其工作原理如图(a)所示,将压敏电阻和一块挡板固定在绝缘小车上,中间放置一个绝缘重球.小车向右做直线运动过程中,电流表示数如图(b)所示,下列判断正确的是( )
 压敏电阻的阻值随所受压力的增大而减小,右位同学利用压敏电阻设计了判断小车运动状态的装置,其工作原理如图(a)所示,将压敏电阻和一块挡板固定在绝缘小车上,中间放置一个绝缘重球.小车向右做直线运动过程中,电流表示数如图(b)所示,下列判断正确的是( )
压敏电阻的阻值随所受压力的增大而减小,右位同学利用压敏电阻设计了判断小车运动状态的装置,其工作原理如图(a)所示,将压敏电阻和一块挡板固定在绝缘小车上,中间放置一个绝缘重球.小车向右做直线运动过程中,电流表示数如图(b)所示,下列判断正确的是( )| A. | 从t1到t2时间内,小车做匀速直线运动 | |
| B. | 从t1到t2时间内,小车做匀加速直线运动 | |
| C. | 从t2到t3时间内,小车做匀速直线运动 | |
| D. | 从t2到t3时间内,小车做匀加速直线运动 |
10.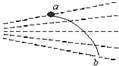 某同学在研究电子在点电荷电场中的运动时,得到了电子由a点运动到b点的轨迹(图中实线所示,虚线是电场线),则下列说法正确的是( )
某同学在研究电子在点电荷电场中的运动时,得到了电子由a点运动到b点的轨迹(图中实线所示,虚线是电场线),则下列说法正确的是( )
 某同学在研究电子在点电荷电场中的运动时,得到了电子由a点运动到b点的轨迹(图中实线所示,虚线是电场线),则下列说法正确的是( )
某同学在研究电子在点电荷电场中的运动时,得到了电子由a点运动到b点的轨迹(图中实线所示,虚线是电场线),则下列说法正确的是( )| A. | 电子在a点动能较小 | B. | 电子在b点的电势能较小 | ||
| C. | a点的场强小于b点的场强 | D. | a点的电势高于b点的电势 |
17.甲乙两人在一幢楼的三楼窗口比赛掷垒球,他们都尽力水平掷出同样的垒球,不计空气阻力,甲掷的水平距离正好是乙的两倍,若乙要想水平掷出相当于甲在三楼窗口掷出的距离,则乙应(不计一楼窗口离地高度)( )
| A. | 在5楼窗口水平掷出 | B. | 在6楼窗口水平掷出 | ||
| C. | 在9楼窗口水平掷出 | D. | 在12楼窗口水平掷出 |
14. 一列横波在t=0时刻的波形如图中实线所示,在t=1s时刻的波形如图中虚线所示.由此可以判定此波的( )
一列横波在t=0时刻的波形如图中实线所示,在t=1s时刻的波形如图中虚线所示.由此可以判定此波的( )
 一列横波在t=0时刻的波形如图中实线所示,在t=1s时刻的波形如图中虚线所示.由此可以判定此波的( )
一列横波在t=0时刻的波形如图中实线所示,在t=1s时刻的波形如图中虚线所示.由此可以判定此波的( )| A. | 波长是4cm | B. | 周期一定是4s | ||
| C. | 传播速度一定是2cm/s | D. | 振幅一定是4cm |
15. 一根轻质弹簧的下端固定在水平地面,上端连接一个小球,静止时小球处于O点,如图所示.将小球向下压至A点位置(未超过弹簧的弹性限度)然后放开,小球将在竖直方向上下往复运动,小球到达的最高位置为B点,忽略空气阻力的影响.则关于小球从A点向上运动至B点的过程中,以下判断正确的是( )
一根轻质弹簧的下端固定在水平地面,上端连接一个小球,静止时小球处于O点,如图所示.将小球向下压至A点位置(未超过弹簧的弹性限度)然后放开,小球将在竖直方向上下往复运动,小球到达的最高位置为B点,忽略空气阻力的影响.则关于小球从A点向上运动至B点的过程中,以下判断正确的是( )
 一根轻质弹簧的下端固定在水平地面,上端连接一个小球,静止时小球处于O点,如图所示.将小球向下压至A点位置(未超过弹簧的弹性限度)然后放开,小球将在竖直方向上下往复运动,小球到达的最高位置为B点,忽略空气阻力的影响.则关于小球从A点向上运动至B点的过程中,以下判断正确的是( )
一根轻质弹簧的下端固定在水平地面,上端连接一个小球,静止时小球处于O点,如图所示.将小球向下压至A点位置(未超过弹簧的弹性限度)然后放开,小球将在竖直方向上下往复运动,小球到达的最高位置为B点,忽略空气阻力的影响.则关于小球从A点向上运动至B点的过程中,以下判断正确的是( )| A. | 弹簧的弹力对小球始终做正功 | |
| B. | 小球在O点时的动能达到最大 | |
| C. | 小球在B点时弹簧的弹性势能最大 | |
| D. | 弹簧的弹性势能与小球的动能之和一定减小 |
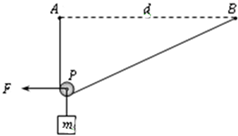 如图所示,将一根长为2d的不可伸长的细绳两端固定在相距为d的AB两等高点,绳上挂一小滑轮P,P下面有一质量为m的物体处于静止状态.现用水平力F拉住滑轮使AP处于竖直方向.若不计绳与滑轮摩擦及空气阻力,也不计绳与滑轮的质量.求水平力F的大小.
如图所示,将一根长为2d的不可伸长的细绳两端固定在相距为d的AB两等高点,绳上挂一小滑轮P,P下面有一质量为m的物体处于静止状态.现用水平力F拉住滑轮使AP处于竖直方向.若不计绳与滑轮摩擦及空气阻力,也不计绳与滑轮的质量.求水平力F的大小. 如图所示,在竖直平面内固定一光滑$\frac{1}{4}$圆弧轨道AB,轨道半径为R=0.4m,轨道最高点A与圆心O等高.有一倾角θ=30°的斜面,斜面底端C点在圆弧轨道B点正下方、距B点H=1.5m.圆弧轨道和斜面均处于场强E=100N/C、竖直向下的匀强电场中.现将一个质量为m=0.02kg、带电量为q=+2×10-3C的带电小球从A点静止释放,小球通过B点离开圆弧轨道沿水平方向飞出,当小球运动到斜面上D点时速度方向恰与斜面垂直,并刚好与一个以一定初速度从斜面底端上滑的不带电的物块相遇.若物块与斜面间动摩擦因数μ=$\frac{\sqrt{3}}{5}$,空气阻力不计,g取10m/s2,小球和物块都可视为质点.求:
如图所示,在竖直平面内固定一光滑$\frac{1}{4}$圆弧轨道AB,轨道半径为R=0.4m,轨道最高点A与圆心O等高.有一倾角θ=30°的斜面,斜面底端C点在圆弧轨道B点正下方、距B点H=1.5m.圆弧轨道和斜面均处于场强E=100N/C、竖直向下的匀强电场中.现将一个质量为m=0.02kg、带电量为q=+2×10-3C的带电小球从A点静止释放,小球通过B点离开圆弧轨道沿水平方向飞出,当小球运动到斜面上D点时速度方向恰与斜面垂直,并刚好与一个以一定初速度从斜面底端上滑的不带电的物块相遇.若物块与斜面间动摩擦因数μ=$\frac{\sqrt{3}}{5}$,空气阻力不计,g取10m/s2,小球和物块都可视为质点.求: