题目内容
13. 如图所示,在竖直平面内固定一光滑$\frac{1}{4}$圆弧轨道AB,轨道半径为R=0.4m,轨道最高点A与圆心O等高.有一倾角θ=30°的斜面,斜面底端C点在圆弧轨道B点正下方、距B点H=1.5m.圆弧轨道和斜面均处于场强E=100N/C、竖直向下的匀强电场中.现将一个质量为m=0.02kg、带电量为q=+2×10-3C的带电小球从A点静止释放,小球通过B点离开圆弧轨道沿水平方向飞出,当小球运动到斜面上D点时速度方向恰与斜面垂直,并刚好与一个以一定初速度从斜面底端上滑的不带电的物块相遇.若物块与斜面间动摩擦因数μ=$\frac{\sqrt{3}}{5}$,空气阻力不计,g取10m/s2,小球和物块都可视为质点.求:
如图所示,在竖直平面内固定一光滑$\frac{1}{4}$圆弧轨道AB,轨道半径为R=0.4m,轨道最高点A与圆心O等高.有一倾角θ=30°的斜面,斜面底端C点在圆弧轨道B点正下方、距B点H=1.5m.圆弧轨道和斜面均处于场强E=100N/C、竖直向下的匀强电场中.现将一个质量为m=0.02kg、带电量为q=+2×10-3C的带电小球从A点静止释放,小球通过B点离开圆弧轨道沿水平方向飞出,当小球运动到斜面上D点时速度方向恰与斜面垂直,并刚好与一个以一定初速度从斜面底端上滑的不带电的物块相遇.若物块与斜面间动摩擦因数μ=$\frac{\sqrt{3}}{5}$,空气阻力不计,g取10m/s2,小球和物块都可视为质点.求:(1)小球经过B点时的速度大小;
(2)B、D两点间竖直高度h;
(3)物块上滑初速度v0满足的条件.
分析 (1)小球从A运动到B的过程,运用动能定理可求出小球到达B点的速度.
(2)小球由B点到D点做类平抛运动,根据D点的速度与斜面垂直,由速度分解和速度时间公式可求出从B到D的时间,由牛顿第二定律和位移公式求出下落的高度h.
(3)根据牛顿第二定律和运动学公式得到物块上滑的位移表达式,结合几何关系可以求出滑块的初速度.
解答 解:(1)设小球到达B点的速度为vB,由动能定理有:
mgR+qER=$\frac{1}{2}$mvB2-0,
代入数据解得:vB=4m/s;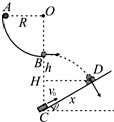
(2)设小球由B点到D点的运动时间为t,加速度为a,下落高度为h有:
tanθ=$\frac{{v}_{B}}{{v}_{y}}$=$\frac{{v}_{B}}{at}$,
由牛顿第二定律得:Eq+mg=ma,h=$\frac{1}{2}$at2,
解得:h=1.2m;
(3)作出小球与物块的运动示意如图所示,设C、D间的距离为x,由几何关系有:x=$\frac{H-h}{sinθ}$,
设物块上滑加速度为a′,由牛顿运动定律有:mgsinθ+μmgcosθ=ma′,
根据题意,要物块与小球相遇,有:$\frac{{v}_{0}^{2}}{2a}$≥x,
解得:v0≥$\frac{4\sqrt{15}}{15}$m≈3.10m/s;
答:(1)小球经过B点时的速度大小为4m/s;
(2)B、D两点间竖直高度h为1.2m.
(3)物块上滑初速度v0满足的条件为v0≥3.10m/s.
点评 本题是复杂的力电综合题,本题关键分析清楚小球和滑块的运动情况,根据类平抛运动速度分解,由力学规律求解.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案
相关题目
1. 如图所示,用甲、乙、丙三个电动势E相同而内电阻r不同的电源,分别给定值电阻R供电.已知甲、乙、丙三个电源内阻的大小关系为:r甲>r乙>r丙,则将R先后接在这三个电源上时的情况相比,下列说法中正确的是( )
如图所示,用甲、乙、丙三个电动势E相同而内电阻r不同的电源,分别给定值电阻R供电.已知甲、乙、丙三个电源内阻的大小关系为:r甲>r乙>r丙,则将R先后接在这三个电源上时的情况相比,下列说法中正确的是( )
 如图所示,用甲、乙、丙三个电动势E相同而内电阻r不同的电源,分别给定值电阻R供电.已知甲、乙、丙三个电源内阻的大小关系为:r甲>r乙>r丙,则将R先后接在这三个电源上时的情况相比,下列说法中正确的是( )
如图所示,用甲、乙、丙三个电动势E相同而内电阻r不同的电源,分别给定值电阻R供电.已知甲、乙、丙三个电源内阻的大小关系为:r甲>r乙>r丙,则将R先后接在这三个电源上时的情况相比,下列说法中正确的是( )| A. | 接在甲电源上时,电源的输出电流最大 | |
| B. | 接在丙电源上时,电源的输出电流最小 | |
| C. | 接在乙电源上时,电阻R消耗的电功率最大 | |
| D. | 接在丙电源上时,电阻R消耗的电功率最大 |
4.学习物理除了知识的学习外,还要领悟并掌握处理物理问题的思想与方法.下列关于物理方法说法不正确的是( )
| A. | 元电荷是一种理想化模型 | |
| B. | 电容不是用比值法定义的物理量 | |
| C. | 运动的合成与分解是等效替代的方法 | |
| D. | 库仑定律的发现是类比了万有引力定律的平方反比关系 |
1. 如图所示,一圆盘可以绕其竖直轴在水平面内运动,圆柱半径为R,甲、乙两物体的质量分别为M和m(M>m),它们与圆盘之间的最大静摩擦力均为正压力的μ倍,两物体用长为L的轻绳连在一起,L<R.若将甲物体放在转轴位置上,甲、乙连线正好沿半径方向拉直,要使两物体与圆盘不发生相对滑动,则圆盘旋转的角速度最大不得超过:(两物体看作质点)( )
如图所示,一圆盘可以绕其竖直轴在水平面内运动,圆柱半径为R,甲、乙两物体的质量分别为M和m(M>m),它们与圆盘之间的最大静摩擦力均为正压力的μ倍,两物体用长为L的轻绳连在一起,L<R.若将甲物体放在转轴位置上,甲、乙连线正好沿半径方向拉直,要使两物体与圆盘不发生相对滑动,则圆盘旋转的角速度最大不得超过:(两物体看作质点)( )
 如图所示,一圆盘可以绕其竖直轴在水平面内运动,圆柱半径为R,甲、乙两物体的质量分别为M和m(M>m),它们与圆盘之间的最大静摩擦力均为正压力的μ倍,两物体用长为L的轻绳连在一起,L<R.若将甲物体放在转轴位置上,甲、乙连线正好沿半径方向拉直,要使两物体与圆盘不发生相对滑动,则圆盘旋转的角速度最大不得超过:(两物体看作质点)( )
如图所示,一圆盘可以绕其竖直轴在水平面内运动,圆柱半径为R,甲、乙两物体的质量分别为M和m(M>m),它们与圆盘之间的最大静摩擦力均为正压力的μ倍,两物体用长为L的轻绳连在一起,L<R.若将甲物体放在转轴位置上,甲、乙连线正好沿半径方向拉直,要使两物体与圆盘不发生相对滑动,则圆盘旋转的角速度最大不得超过:(两物体看作质点)( )| A. | $\sqrt{\frac{μ(M-m)g}{mL}}$ | B. | $\sqrt{\frac{μ(M-m)g}{ML}}$ | C. | $\sqrt{\frac{μ(M+m)g}{ML}}$ | D. | $\sqrt{\frac{μ(M+m)g}{mL}}$ |
3.两个材料相同的物体,甲的质量大于乙的质量,以相同的初动能在同一水平面上滑动,最后都静止,它们在水平面上滑行的距离的大小关系是( )
| A. | 乙大 | B. | 甲大 | C. | 一样大 | D. | 无法比较 |
 如图9所示,在磁感应强度B=0.5T的匀强磁场中,让长L=0.2m的导体AB在金属框上以υ=5m/s的速度向右滑动.如果R1=2Ω,R2=1Ω,其他导线上的电阻忽略不计.求通过AB的电流大小.
如图9所示,在磁感应强度B=0.5T的匀强磁场中,让长L=0.2m的导体AB在金属框上以υ=5m/s的速度向右滑动.如果R1=2Ω,R2=1Ω,其他导线上的电阻忽略不计.求通过AB的电流大小. 如图所示,在水平面固定一倾角θ=30°的光滑斜面(水平面与斜面用一小段圆弧相连),一光滑木块甲从斜面上高h=5cm的A点由静止释放,同时一木块乙在水平面的C点已初速度v0向右运动,经过时间t=1s,两木块在水平面上相碰.已知C点到斜面底端B的距离L=3.8m,木块乙与水平面间的动摩擦因数μ=0.2,取g=10m/s2,求木块乙的初速度v0.
如图所示,在水平面固定一倾角θ=30°的光滑斜面(水平面与斜面用一小段圆弧相连),一光滑木块甲从斜面上高h=5cm的A点由静止释放,同时一木块乙在水平面的C点已初速度v0向右运动,经过时间t=1s,两木块在水平面上相碰.已知C点到斜面底端B的距离L=3.8m,木块乙与水平面间的动摩擦因数μ=0.2,取g=10m/s2,求木块乙的初速度v0. 如图所示,电灯的质量m=0.1kg,绳与顶板间的夹角为45°度,灯泡处于静止状态,绳OB水平,则绳OA所受的拉力F1是多少?绳OB所受的拉力F2是多少?(g取10m/s2)
如图所示,电灯的质量m=0.1kg,绳与顶板间的夹角为45°度,灯泡处于静止状态,绳OB水平,则绳OA所受的拉力F1是多少?绳OB所受的拉力F2是多少?(g取10m/s2)