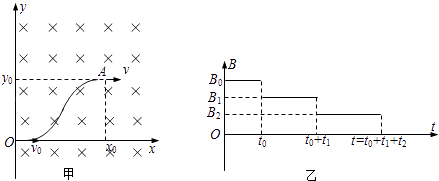��Ŀ����
����Ŀ����ͼ��ʾ��ֱ���ڣ�ˮƽ��OO���·��㹻��������ڴ���ˮƽ��ǿ�ų����Ÿ�Ӧǿ��ΪB��һ�����������ε���߳�ΪL������Ϊm���ܵ���Ϊr����ab�߾���߽�OO��ΪL��λ���ɾ�ֹ�ͷţ���֪��ab�߸ս���ų���cd�߸ս���ų�����ʱ��t���������ٶ�Ϊg�������������ƣ������ת����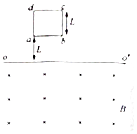
��1��ab�߸ս���ų�ʱ��ba����Ʋ�Ĵ�СUba��
��2��cd�߸ս���ų�ʱ���������ٶȣ�
���𰸡�
��1���⣺��ab�߸ս���ų�ʱ���ٶ�Ϊv1�����ݻ�е���غ㶨�ɿɵã�
mgL= ![]() ��
��
���ݷ����ڵ�Ÿ�Ӧ���ɿɵò����ĸ�Ӧ�綯��Ϊ��
E1=BLv1��
��ʱ�ĸ�Ӧ����Ϊ��
I= ![]() ��
��
����ba����Ʋ�Ĵ�СUba= ![]() ��
��
��ab�߸ս���ų�ʱ��ba����Ʋ�Ĵ�СΪ ![]() ��
��
��2����ab�߸ս���ų���cd�߸ս���ų��Ĺ����У����ݶ��������ɵã�
mgt��B ![]() Lt=mv2��mv1��
Lt=mv2��mv1��
����B ![]() Lt=
Lt= ![]() =
= ![]() ��
��
��ã�v2=gt�� ![]() +
+ ![]() ��
��
��cd�߸ս���ų�ʱ���������ٶ�Ϊgt�� ![]() +
+ ![]() ��
��
����������1�����ݻ�е���غ㶨�ɼ����߿�ս���ų�ʱ���ٶȣ��ٸ��ݱպϵ�·��ŷķ���ɺ͵�ѹ�����ص���⣻
��2�����ݶ��������з��̣��ټ����ƽ���������Ĵ�С�����ɵõ��������ٶȣ�

��ϰ��ϵ�д�
�����Ŀ