题目内容
【题目】1772年,法籍意大利数学家拉格朗日在论文《三体问题》指出:两个质量相差悬殊的天体(如太阳和地球)所在同一平面上有5个特殊点,如图中的L1、L2、L3、L4、L5所示,人们称为拉格朗日点.若飞行器位于这些点上,会在太阳与地球共同引力作用下,可以几乎不消耗燃料而保持与地球同步绕太阳做圆周运动.若发射一颗卫星定位于拉格朗日L2点,下列说法正确的是( )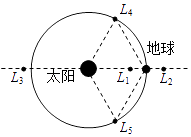
A.该卫星绕太阳运动周期和地球自转周期相等
B.该卫星在L2点处于平衡状态
C.该卫星绕太阳运动的向心加速度大于地球绕太阳运动的向心加速度
D.该卫星在L2处所受太阳和地球引力的合力比在L1处大
【答案】C,D
【解析】解:A、据题意知,卫星与地球同步绕太阳做圆周运动,则周期相同,即该卫星绕太阳运动周期和地球公转周期相等,A不符合题意.
B、该卫星所受的合力为地球和太阳对它引力的合力,这两个引力方向相同,合力不为零,处于非平衡状态,B不符合题意 .
C、向心加速度a=ω2r,该卫星和地球绕太阳做匀速圆周运动的角速度相对,而半径大于地球公转半径,则该卫星绕太阳运动的向心加速度大于地球绕太阳运动的向心加速度,C符合题意.
D、该卫星在L2处和L1处的角速度相等,但在L2处半径大,根据F=mω2r可知,该卫星在L2处所受太阳和地球引力的合力比在L1处大,D符合题意.
故答案为:CD
卫星与地球绕太阳运动的周期和频率都相同,一定处于非平衡状态,根据匀速圆周运动的公式,求解。

练习册系列答案
相关题目