��Ŀ����
����Ŀ����ͼ��ʾ���⻬ˮƽ��AB����ֱ���ڵİ�Բ�ε�����B����ӣ�����뾶ΪR��һ������Ϊm�����彫����ѹ����A����ɾ�ֹ�ͷţ��ڵ���������������ijһ�����ٶȺ����뵯�ɣ����뵯�ɺ�������B����뵼��˲��Ե����ѹ��Ϊ��������7����֮�������˶���ɰ��Բ���˶�ǡ�õ���C�㣮����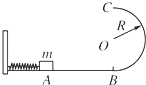
��1�����ɿ�ʼʱ�ĵ������ܣ�
��2�������B���˶���C��˷��������Ĺ���
��3�������뿪C������ˮƽ��ʱ���ٶȴ�С�ͷ���
���𰸡�
��1���⣺�����B��ʱ����ţ�ٵڶ����ɵã�FN��mg=m ![]() ��
��
�����⣺FN=7mg
���徭��B��Ķ��ܣ�EkB= ![]() mvB2=3mgR
mvB2=3mgR
�������A����B��Ĺ����У����ݻ�е���غ㶨�ɣ����ɵĵ������ܣ�Ep=EkB=3mgR
�𣺵��ɿ�ʼʱ�ĵ���������3mgR
��2���⣺���嵽��C���������mg������ţ�ٵڶ������У�mg=m ![]() ��EkC=
��EkC= ![]() mvC2=
mvC2= ![]() mgR
mgR
�����B�㵽C��ֻ���������������������ݶ��ܶ����У�W����mg2R=EkC��EkB
��ã�W��=��0.5mgR
���������B���˶���C��˷��������Ĺ�Ϊ��W=0.5mgR
�������B���˶���C��˷��������Ĺ�Ϊ0.5mgR
��3���⣺�����뿪�������ƽ���˶���
ˮƽ�����У� ![]()
��ֱ�����У� ![]()
���ʱ���ٶȴ�С�� ![]()
��ˮƽ����ɦȽ�б���£� ![]() ���æ�=arctan2
���æ�=arctan2
�������뿪C������ˮƽ��ʱ���ٶȴ�С�� ![]() ��������ˮƽ�����arctan2��
��������ˮƽ�����arctan2��
����������1���о����徭��B���״̬������ţ���˶�����������徭��B����ٶȣ��õ�����Ķ��ܣ������A����B��Ĺ����л�е���غ㶨�ɣ����ɵĵ������ܵ����徭��B��Ķ��ܣ���2������ǡ�õ���C��ʱ���������䵱����������ţ�ٵڶ��������C����ٶȣ������B��C�Ĺ��̣����ö��ܶ������˷��������Ĺ�����3�������뿪�������ƽ���˶��������˶��ĺϳɺͷֽⷨ��������뿪C������ˮƽ��ʱ���ٶȴ�С�ͷ���
�����㾫����������Ŀ����֪����������ƽ���˶��ͻ�е���ۺ�Ӧ�õ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ�����ص�:�پ���ˮƽ����ij��ٶ�;��ֻ���������ã��Ǽ��ٶ�Ϊ�������ٶ�g���ȱ��������˶����˶�����:ƽ���˶����Էֽ�Ϊˮƽ���������ֱ���˶�����ֱ��������������˶���ϵͳ��̬���ܻ�е��E 1 ����ĩ̬���ܻ�е��E 2 ����E1 =E2��ϵͳ���ٵ����������ܦ�E P�� ����ϵͳ���ӵ��ܶ��ܦ�E K�� ������E P�� =��E K������ϵͳֻ��A��

 ������ȫ�̼����ĩ���100��ϵ�д�
������ȫ�̼����ĩ���100��ϵ�д�