题目内容
【题目】如图甲所示,y轴右侧空间有垂直xoy平面向里的匀强磁场,同时还有沿﹣y方向的匀强电场(图中电场未画出).磁感应强度随时间变化规律如图乙所示(图中B0已知,其余量均为未知).t=0时刻,一质量为m、电荷量为+q的带电粒子以速度v0从坐标原点O沿x轴射入电场和磁场区,t0时刻粒子到达坐标为(x0 , y0)的点A (x0>y0),速度大小为v,方向沿+x方向,此时撤去电场.t=t0+t1+t2时刻,粒子经过x轴上x=x0点,速度沿+x方向.不计粒子重力,求: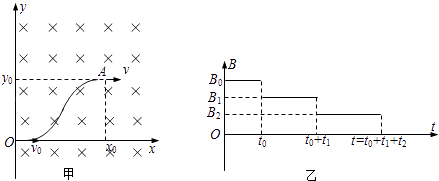
(1)0﹣t0时间内OA两点间电势差UOA;
(2)粒子在t=0时刻的加速度大小a0;
(3)B1的最小值及对应t2的表达式.
【答案】
(1)解:带电粒子由O到A运动过程中,由动能定理得:
qUOA= ![]() mv2﹣
mv2﹣ ![]() mv02,
mv02,
解得:UOA= ![]() ;
;
答:0﹣t0时间内OA两点间电势差UOA为 ![]() ;
;
(2)设电场强度大小为E,则有:UAO=Ey0,
t=0时刻,由牛顿第二定律得:qv0B0﹣qE=ma0,
解得:a0= ![]() ﹣
﹣ ![]() ;
;
答:粒子在t=0时刻的加速度大小a0为 ![]() ﹣
﹣ ![]() ;
;
(3)t0~t0+t1时间内,粒子在小的虚线圆上运动,t0+t1时刻粒子从C点切入大圆,大圆最大半径为x0,相应小圆最大半径为R,
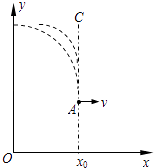
由几何知识得:R= ![]() ,
,
由牛顿第二定律得:qvB1=m ![]() ,
,
B1的最小值:Bmin= ![]() ,
,
对应于B1取最小值,带电粒子由C点到经过x轴上x=x0点的时间t2满足t2=(k+ ![]() )
) ![]() (k=0,1,2…);
(k=0,1,2…);
答:B1的最小值为 ![]() ,对应t2的表达式为:t2=(k+
,对应t2的表达式为:t2=(k+ ![]() )
) ![]() (k=0,1,2…).
(k=0,1,2…).
【解析】(1)粒子从O到A过程,根据动能定理和电势差的公式可以直接求出两点间的电压.
(2)根据匀强电场场强度和电势差的关系,求场强和电场力,再根据牛顿第二定律可以求出粒子的加速度.
(3)作出粒子运动轨迹,由几何知识求出粒子的轨道半径,粒子在磁场中做匀速圆周运动洛伦兹力提供向心力,应用牛顿第二定律可以求出磁感应强度.