题目内容
【题目】如图所示,在竖直平面内,AB为水平放置的绝缘粗糙轨道,CD为竖直放置的足够长绝缘光滑轨道,AB与CD通过四分之一绝缘光滑圆弧形轨道平滑连接,圆弧的圆心为O,半径R=0.50m,轨道所在空间存在水平向右的匀强电场,电场强度的大小E=2.0×104N/C,现有质量m=0.20kg,电荷量q=+4.0×10-4C的带电体(可视为质点),从A点由静止开始运动,已知SAB=1.0m,带电体与轨道AB的动摩擦因数均为0.5.(取g=10m/s2)求:
(I)带电体运动到圆弧形轨道C点时的速度;
(2)带电体上升时距离AB的最大高度
(3)带电体返回B点时立刻撤去电场,其他条件不变,则带电体停在距离B点多远处.

【答案】(1)10m/s (2)5.5m (3)7m
【解析】
(1)设带电体到达C时的速度为![]() ,有动能定理得:
,有动能定理得:
![]()
解得
v=10 m/s
(2)带电体到达C点后做竖直上抛运动
mgh=![]() mv2
mv2
得
h=5m
即带电体上升时距离AB的最大高度为
h+R=5.5m
(3)由能量守恒定律可知带电体返回到B点时的速度即为最初从A到B时的速度vB,由动能定理得:
qESAB-μmgSAB=![]() mvB2
mvB2
之后撤去电场则有
![]() mvB2=μmgS
mvB2=μmgS
解得
S=7m

【题目】某同学用下图装置做“研究匀变速直线运动”的实验,得到一条用电火花计时器打下的纸带如图所示,并在其上取了A、B、C、D、E、F、G 7个计数点,每相邻两个计数点间还有4个点图中没有画出,电火花计时器接220V、50Hz交流电源.
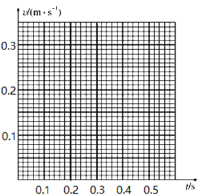
(1)设相邻两计数点间的时间间隔为T,计算E点的瞬时速度vE的表达式为vE=_____;(用图中d1~d6及T表示)


(2)他经过测量并计算得到电火花计时器在打B、C、D、E、F各点时物体的瞬时速度如下表.
对应点 | B | C | D | E | F |
速度(m/s) | 0.141 | 0.180 | 0.218 | 0.262 | 0.301 |
以A点对应的时刻为t=0,试在下图所示坐标系中合理地选择标度,作出v-t图象, (______),并利用该图象求出物体的加速度a=_____m/s2;(保留两位有效数字)
(3)如果当时电网中交变电流的电压变成210 V,而做实验的同学并不知道,那么加速度的测量值与实际值相比______.(填“偏大”、“偏小”或“不变”)