题目内容

（12分）如图，一个质量为m的小球（可视为质点）以某一初速度从A点水平抛出，恰好从圆管BCD的B点沿切线方向进入圆弧，经BCD从圆管的最高点D射出，恰好又落到B点．已知圆弧的半径为R且A与D在同一水平线上，BC弧对应的圆心角θ=60°，不计空气阻力．求：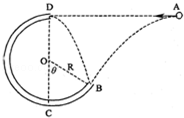

（1）小球从A点做平抛运动的初速度v0的大小；
（2）在D点处管壁对小球的作用力N；
（3）小球在圆管中运动时克服阻力做的功Wf．

（1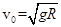）（2）方向竖直向上 （3）

解析试题分析：（1）小球从A到B为平抛运动
竖直方向自由落体即匀变速直线运动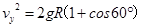
则
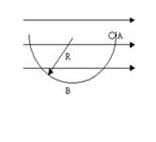
在B点，合速度沿切线方向，速度合成如下图

由速度的几何关系可得 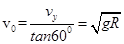       (3分)
（2）小球从D点离开轨道又落回到B此运动仍然是平抛运动：
竖直方向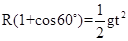      解得： 
水平方向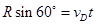
则小球从D点抛出的速度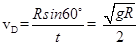
在D点，重力和弹力的合力提供向心力公式即：
解得： 方向竖直向上        (6分)
（3）从A点运动到D点的过程，只有阻力做功，根据动能定理有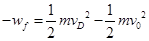

解得
考点：平抛运动 圆周运动 动能定理

练习册系列答案
相关题目

探究能力是进行物理学研究的重要能力之一.物体因绕轴转动而具有的动能叫转动动能，转动动能的大小与物体转动的角速度有关.为了研究某一砂轮的转动动能Ek与角速度ω的关系，某同学采用了下述实验方法进行探索.如图所示，先让砂轮由动力带动匀速旋转，测得其角速度ω，然后让砂轮脱离动力，由于克服转轴间摩擦力做功，砂轮最后停下，测出砂轮脱离动力到停止转动的圈数n，通过分析实验数据得出结论.另外已测试砂轮转轴的直径为2 cm，转轴间的摩擦力为10 N/π.经实验测得的几组ω和n如下表所示:

ω/rad·s-1
0.5
1
2
3
4
n
5.0
20
80
180
320
Ek
 
 
 
 
 

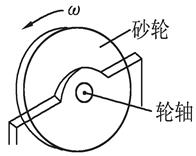
(1)计算出砂轮每次脱离动力的转动动能，并填入上表中.
(2)由上述数据推导出该砂轮的转动动能Ek与角速度ω的关系式为        .
(3)若测得脱离动力后砂轮的角速度为2.5 rad/s，则它转过45圈时的角速度为           rad/s 。

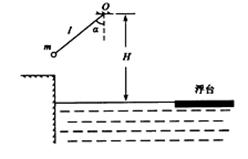
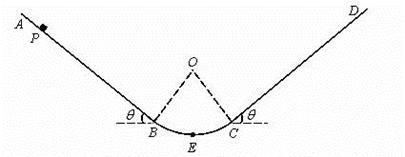
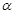在游乐节目中，选手需要借助悬挂在高处的绳飞越到水面的浮台上，小明和小阳观看后对此进行了讨论。如图所示，他们将选手简化为质量m=60kg的质点， 选手抓住绳由静止开始摆动，此时绳与竖直方向夹角=53o，绳的悬挂点O距水面的高度为H=3m.不考虑空气阻力和绳的质量，浮台露出水面的高度不计，水足够深。取重力加速度， (，)

(1)求选手摆到最低点时对绳拉力的大小F；
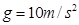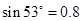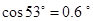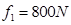(2)若绳长L="2m," 选手摆到最高点时松手落入水中。设水对选手的平均浮力，平均阻力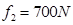，求选手落入水中的深度；
(3)若选手摆到最低点时松手，小明认为绳越长，在浮台上的落点距岸边越远；小阳认为绳越短，落点距岸边越远，请通过推算说明你的观点。

如图所示，固定斜面AB、CD与竖直光滑圆弧BC相切于B、C点，两斜面的倾角θ=37°，圆弧BC半径R=2m．一质量m=1kg的小滑块（视为质点）从斜面AB上的P点由静止沿斜面下滑，经圆弧BC冲上斜面CD．已知P点与斜面底端B间的距离L1=6m，滑块与两斜面间的动摩擦因数均为μ=0.25，g=10m/s2．求：

（1）小滑块第1次经过圆弧最低点E时对圆弧轨道的压力；
（2）小滑块从静止开始下滑到第n次到达B点的过程中在斜面AB上运动通过的总路程．

由相同材料的木板搭成的轨道如图，其中木板AB、BC、CD、DE、EF┅长均为L=1.5m，木板OA和其它木板与水平地面的夹角都为β=370（sin370=0.6，con370=0.8），一个可看成质点的物体在木板OA上从图中的离地高度h=1.8m处由静止释放，物体与木板的动摩擦因数都为μ=0.2，在两木板交接处都用小曲面相连，使物体能顺利地经过它，既不损失动能，也不会脱离轨道。在以后的运动过程中，重力加速度取10m/s2，问：

（1）物体能否静止在木板上？请说明理由。
（2）物体运动的总路程是多少？
（3）物体最终停在何处？并作出解释。

（10分）如图所示，轻杆AB长l，两端各连接A、B小球，质量均为m，杆可以绕距B端l/3处的O轴在竖直平面内自由转动。轻杆由水平位置从静止开始转到竖直方向，求：

（1）此过程中杆对A球做的功是多少。
（2）在竖直方向时转轴O受的作用力大小及方向．（重力加速度为g,不计一切阻力）

(12分)如图所示，足够长的光滑斜面的倾角为37°，质量分别为mA和mB的A、B两小物体用跨过斜面顶端光滑小滑轮的细绳相连，且mA＝3mB。开始时A物体离地高为h＝0.5m，物体B恰在斜面底端，从图示位置由静止开始释放A物体，取g＝10m/s2，sin37°＝0.6，cos37°＝0.8。求：

⑴A物体刚要着地时的B的速度大小；
⑵B物体在斜面上上升的最远距离。

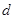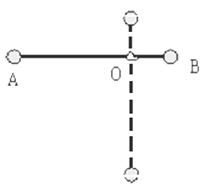
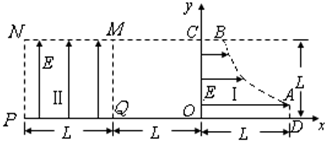
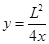如图所示为研究电子枪中电子在电场中运动的简化模型示意图．在Oxy平面的第一象限，存在以x轴y轴及双曲线的一段（0≤x≤L，0≤y≤L）为边界的匀强电场I；在第二象限存在以x=-L； x=-2L；y=0；y=L的匀强电场II．两个电场大小均为E，不计电子所受重力．求

（1）从电场I的边界B点处由静止释放电子，电子离开MNPQ时的位置;
（2）由电场I的AB曲线边界处由静止释放电子离开MNPQ时的最小动能；

光滑绝缘半球槽的半径为R，处在水平向右的匀强电场中，一质量为m的带电小球从槽的右端A处（与球心等高）无初速沿轨道滑下，滑到最低点B时，球对轨道的压力为2mg。求

（1）小球从A到B的过程中受到的电场力做的功及电场力的大小
（2）带电小球在滑动过程中的最大速度

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网