题目内容
(18分)如图所示,一电子(其重力不计,质量为m、电荷量为e,由静止开始,经加速电场加速后,水平向右从两板正中间射入偏转电场.偏转电场由两块水平平行放置的长为l相距为d的导体板组成,当两板不带电时,电子通过两板之间的时间均为t0,当在两板间加电压为U0时,电子可射出偏转电场,并射入垂直纸面向里的匀强磁场,最后打在磁场右侧竖直放置的荧光屏上.磁场的水平宽度为s,竖直高度足够大。求:
(1)加速电场的电压;
(2)电子在离开偏转电场时的侧向位移;
(3)要使电子能垂直打在荧光屏上,匀强磁场的磁感应强度为多大?
(1) (2)
(2)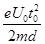 (3)
(3)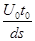
解析试题分析:(1)电子离开加速电场时的速度为 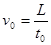 ┅┅┅┅┅┅┅┅(2分)
┅┅┅┅┅┅┅┅(2分)
由动能定理得 ┅┅┅┅┅┅┅┅┅┅┅┅(2分)
┅┅┅┅┅┅┅┅┅┅┅┅(2分)
得 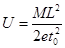 ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅(1分)
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅(1分)
(2)电子进入偏转电场E=U0/d (1分)
F="Ee" =ma ┅┅┅┅┅┅(2分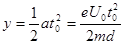 ┅┅┅┅┅┅┅┅┅┅┅(2分)
┅┅┅┅┅┅┅┅┅┅┅(2分)
(3)设电子从偏转电场中射出时的偏向角为θ,要电子垂直打在荧光屏上,则电子在磁场中运动半径为: 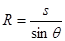 ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅(1分)
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅(1分)
设电子从偏转电场中出来时的速度为v,垂直偏转极板的速度为vy,则电子从偏转电场中出来时的偏向角为: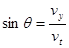 ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅(1分)
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅(1分)
式中 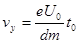 ┅┅┅(2分)
┅┅┅(2分)
又 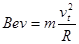 ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ (2分)
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅ (2分)
由上述可得: ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅(2分)
┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅(2分)
(如果电量用q表示,扣1分)
考点:带电粒子在电、磁场中的运动 动能定理 牛顿第二定律

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案某人蹲在台秤上,当他突然站起的过程中,关于台秤示数的变化判断正确的是( )
| A.一直变小 |
| B.先变大后变小,最后恢复到蹲在台秤时相同示数 |
| C.一直变大 |
| D.先变小后变大,最后恢复到蹲在台秤时相同示数 |
如图所示,在第二象限内有水平向右的匀强电场,电场强度为E,在第一、第四象限内分别存在如图所示的匀强磁场,磁感应强度大小相等。有一个带电粒子以初速度v0垂直x轴,从x轴上的P点进入匀强电场,恰好与y轴成45°角射出电场,再经过一段时间又恰好垂直于x轴进入下面的磁场。已知OP之间的距离为d,则带电粒子( )
A.在电场中运动的时间为 |
B.在磁场中做圆周运动的半径为 |
C.自进入磁场至第二次经过x轴所用时间为 |
D.自进入电场至在磁场中第二次经过x轴的时间为 |

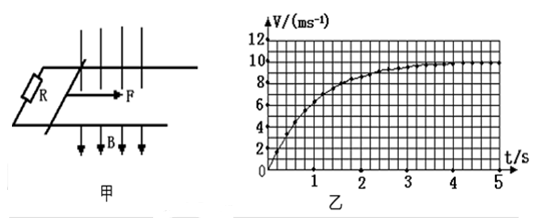

 ;
;
 L。现在一群质量为m、电荷量大小为q(重力不计)的带电粒子,分布在A、B之间。t=0时刻,这群带电粒子以相同的初速度v0沿x轴正方向开始运动。观察到从A点出发的带电粒子恰好从D点第一次进入磁场,然后从O点第一次离开磁场。
L。现在一群质量为m、电荷量大小为q(重力不计)的带电粒子,分布在A、B之间。t=0时刻,这群带电粒子以相同的初速度v0沿x轴正方向开始运动。观察到从A点出发的带电粒子恰好从D点第一次进入磁场,然后从O点第一次离开磁场。