题目内容
（12分）如图甲所示，放置在水平桌面上的两条光滑导轨间的距离L=1m，质量m=1kg的光滑导体棒放在导轨上，导轨左端与阻值R=4Ω的电阻相连，导体棒及导轨的电阻不计，所在位置有磁感应强度为B=2T的匀强磁场，磁场的方向垂直导轨平面向下。现在给导体棒施加一个水平向右的恒定拉力F，并每隔0.2s测量一次导体棒的速度，乙图是根据所测数据描绘出导体棒的v-t图象。设导轨足够长，求：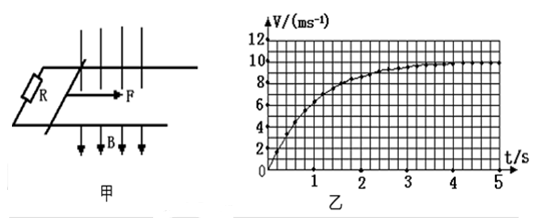
（1）力F的大小；
（2）t =1.2s时，导体棒的加速度；
（3）估算1.6s内电阻R上产生的热量。
（1）10N （2）3m/s2 （3）48J
解析试题分析：（1）由图可知，导体棒运动的速度达到10m/s时开始做匀速运动，此时安培力和拉力F大小相等。导体棒匀速运动的速度
匀速运动后导体棒上的电动势：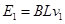
(1分)
导体棒受的安培力：
(2分)
则：
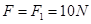(1分)
（2）由图可知，时间t=1.2s时导体棒的速度
此时导体棒上的电动势：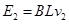
(1分)
导体棒受的安培力：
＝
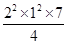N＝7N (2分)
由牛顿定律得：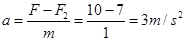
(1分)
（3）由图知，到1.6s处，图线下方小方格的个数为40个，每个小方格代表的位移为
所以1.6s内导体棒的位移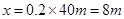 
(2分)
拉力F做功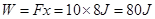 
(1分)
由图知此时导体棒的速度 
导体棒动能 
根据能量守恒定律，产生的热量
(1分)
（说明：格数为39~42均正确 ，答案范围46 ~52J ）
考点：安培力 电磁感应定律 能量守恒
阅读快车系列答案质量分别为m1和m2的两个物体用一个未发生形变的弹簧连接，如图所示，让它们从高处同时自由下落，则下落过程中弹簧发生的形变是(不计空气阻力)( )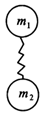
| A．若m1＞m2，则弹簧将被压缩 |
| B．若m1＜m2，则弹簧将被拉长 |
| C．只有m1＝m2，弹簧才会保持原长 |
| D．无论m1和m2为何值，弹簧长度均不变 |
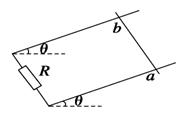
两根相距为L的足够长的金属弯角光滑导轨如图所示放置，它们各有一边在同一水平面内，另一边与水平面的夹角为37°，质量均为m的金属细杆ab、cd与导轨垂直接触形成闭合回路，导轨的电阻不计，回路总电阻为2R，整个装置处于磁感应强度大小为B，方向竖直向上的匀强磁场中，当ab杆在平行于水平导轨的拉力F作用下以速度v沿导轨匀速运动时，cd杆恰好处于静止状态，重力加速度为g，以下说法正确的是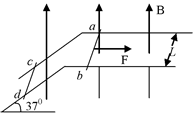
| A．ab杆所受拉力F的大小为mgtan37° |
B．回路中电流为 |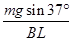
| C．回路中电流的总功率为mgv sin37° |
D．m与v大小的关系为m＝ |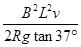
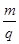＝4×10－10 kg/C的带正电粒子从x轴上的A点以初速度v0＝2×107 m/s垂直x轴射入电场，OA＝0.2 m，不计重力．求：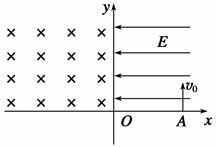
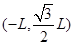，带电粒子质量为m，电荷量为q，初速度为v0，不计粒子重力。求：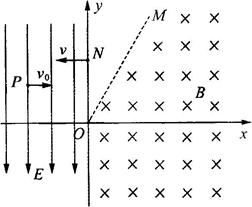
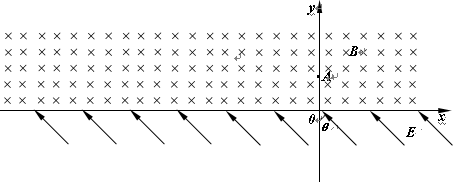
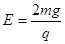。一质量为m、电荷量为+q的带电小环穿在轨道内，它与两根直轨道间的动摩擦因数为μ（0<μ<1），而轨道的圆弧形部分均光滑。将小环在较长的直轨道CD下端的C点无初速释放（不考虑电场和磁场的边界效应，重力加速度为g），求：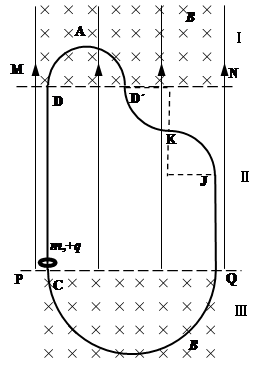
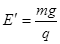，则小环在两根直轨道上通过的总路程多大？