题目内容
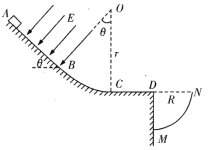
【题目】如图所示，ABCD为固定在竖直平面内的轨道，AB段平直倾斜且粗糙，BC段是光滑圆弧，对应的圆心角
，半径为r，CD段水平粗糙，各段轨道均平滑连接，在D点右侧固定了一个
圆弧挡板MN，圆弧半径为R，圆弧的圆心也在D点。倾斜轨道所在区域有场强大小为
、方向垂直于斜轨向下的匀强电场。一个质量为m、电荷量为q的带正电小物块(视为质点)在倾斜轨道上的A点由静止释放，最终从D点水平抛出并击中挡板。已知A，B之间距离为2r，斜轨与小物块之的动摩擦因数为
，设小物块的电荷量保持不变，重力加速度为g，
，
。求：
(1)小物块运动至圆轨道的C点时对轨道的压力大小；
(2)改变AB之间的距离和场强E的大小，使小物块每次都能从D点以不同的速度水平抛出并击中挡板的不同位置，求击中挡板时小物块动能的最小值。
【答案】（1）在C点小物块对圆轨道的压力大小为
；（2）小物块动能的最小值为
【解析】
(1)小物块由A到B过程由动能定理，得：
解得：
小物块由B到C过程由机械能守恒定律得：
解得：
在C点由牛顿第二定律，得：
解得：
由牛顿第三定律可得，在C点小物块对圆轨道的压力大小为
(2)小物块离开D点后做平抛运动，水平方向：
竖直方向：
而：
小物块平抛过程机械能守恒，得：
由以上式子得：
由数学中均值不等式可知：
则小物块动能的最小值为
练习册系列答案
相关题目
