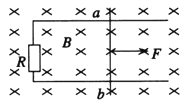
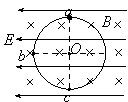题目内容
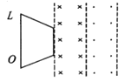
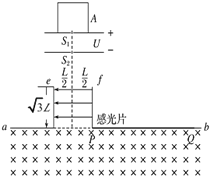
【题目】如图所示，容器A中装有大量的质量不同、电荷量均为+q的粒子，粒子从容器下方的小孔S1不断飘入加速电场（初速度可视为零）做直线运动，通过小孔S2后从两平行板中央垂直电场方向射入偏转电场。粒子通过平行板后垂直磁场方向进入磁感应强度为B、方向垂直纸面向里的水平匀强磁场区域，最后打在感光片上。已知加速电场中S1、S2间的加速电压为U，偏转电场极板长为
，两板间距为L，板间电场看成匀强电场，其电场强度
，方向水平向左（忽略板间外的电场），平行板f的下端与磁场水平边界ab相交于点P，在边界ab上实线处固定放置感光片。测得从容器A中逸出的所有粒子均打在感光片P、Q之间，且PQ的长度为3L边界ab下方的磁场范围足够大，不考虑粒子所受重力与粒子间的相互作用。求：
（1）粒子射出偏转电场时沿垂直于板面方向偏转的距离x和偏转的角度θ；
（2）射到感光片P处的粒子的质量m1；
（3）粒子在磁场中运动的最长时间tm。
【答案】（1）
；
（2）
（3）
【解析】
（1）粒子先经过加速电场的加速后进入水平匀强电场做类平抛运动，根据平抛运动规律求出偏转距离x和偏转角，这是为后续计算做一个铺垫；
（2）粒子从e板下端与水平方向成60°的角射入匀强磁场，偏转240°后打在P点，由几何关系求出粒子做匀速圆周运动的半径，再由洛仑兹力提供向心力就能求出粒子的质量；
（3）先判断出打在何处的粒子的时间最短，由于t=
T，即质量最大的粒子时间最长，再由半径公式
知质量最大则半径最小，所以打在P点的粒子时间最长，再利用周期公式结合粒子转过的圆心角即可求出粒子在磁场中运动的最长时间。
（1）设质量为m的粒子通过孔S2的速度为v0由动能定理有：qU＝
mv02
粒子在偏转电场中运动的加速度为：
沿速度v0方向 
L＝v0t
沿电场方向 vs＝at，x＝at2
且有 tanθ＝
解得 x＝
．θ＝30°
（2）粒子从e板下方与水平方向成60°角射入匀强磁场。设粒子射入磁场时速度v1．做园周运动的轨道半径为r1，则 qv1B＝m1
其中
由几何关系可知 
解得m1＝
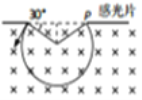
（3）粒子在磁场中做圆周运动的周期 T＝
粒子进入磁场后偏转240°，运动的时间t＝
T
由于qvB＝m
联立解得 t＝
由何关系可知拉子做圆周运动的最大半径 
则tm＝
