题目内容
19.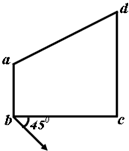 如图所示,a、b、c、d为某匀强电场中的四个点,且ab∥cd、ab⊥bc,bc=cd=2ab=2l,电场线与四边形所在平面平行.已知φa=20V,φb=24V,φd=8V.一个质子经过b点的速度大小为v0,方向与bc夹角为45°,一段时间后经过c点,不计质子的重力,则( )
如图所示,a、b、c、d为某匀强电场中的四个点,且ab∥cd、ab⊥bc,bc=cd=2ab=2l,电场线与四边形所在平面平行.已知φa=20V,φb=24V,φd=8V.一个质子经过b点的速度大小为v0,方向与bc夹角为45°,一段时间后经过c点,不计质子的重力,则( )| A. | c点电势为16V | |
| B. | 场强的方向由a指向d | |
| C. | 质子从b运动到c所用的时间为$\frac{\sqrt{2}l}{{v}_{0}}$ | |
| D. | 质子运动到c时的速度大小为$\sqrt{2}$v0 |
分析 连接bd,bd连线的中点O电势与C点相等,是16V;质子从b→c做类平抛运动,根据v0方向的分位移为$\sqrt{2}$l,求出时间;作出等势线oc,y就能判断场强方向;根据动能定理可求出b到c电场力做的功,结合动能定理求得速度
解答 解: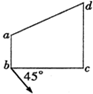 A、三角形bcd是等腰直角三角形,具有对称性,bd连线中点o的电势与c相等,为16V.故A正确.
A、三角形bcd是等腰直角三角形,具有对称性,bd连线中点o的电势与c相等,为16V.故A正确.
B、oc为等势线,其垂线bd为场强方向,b→d,故B错误
C、质子从b→c做类平抛运动,沿初速度方向分位移为$\sqrt{2}$l,此方向做匀速直线运动,则t=$\frac{\sqrt{2}l}{{v}_{0}}$,则C正确.
D、电势差Ubc=8V,则质子从b→c电场力做功为8eV.根据动能定理可得$8eV=\frac{1}{2}m{v}^{2}-\frac{1}{2}{mv}_{0}^{2}$,故D错误.
故选:AC
点评 本题关键是找等势点,作等势线,并抓住等势线与电场线垂直的特点,问题就变得简单明晰

练习册系列答案
相关题目
9.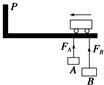 如图,天车下吊着两个质量都是m的工件A和B,整体一起向左匀速运动.系A的吊绳较短,系B的吊绳较长,若天车运动到P处时突然停止,则两吊绳所受拉力FA、FB的大小关系是( )
如图,天车下吊着两个质量都是m的工件A和B,整体一起向左匀速运动.系A的吊绳较短,系B的吊绳较长,若天车运动到P处时突然停止,则两吊绳所受拉力FA、FB的大小关系是( )
 如图,天车下吊着两个质量都是m的工件A和B,整体一起向左匀速运动.系A的吊绳较短,系B的吊绳较长,若天车运动到P处时突然停止,则两吊绳所受拉力FA、FB的大小关系是( )
如图,天车下吊着两个质量都是m的工件A和B,整体一起向左匀速运动.系A的吊绳较短,系B的吊绳较长,若天车运动到P处时突然停止,则两吊绳所受拉力FA、FB的大小关系是( )| A. | FA>FB>mg | B. | FA<FB<mg | C. | FA=FB=mg | D. | Fa=FB>mg |
10.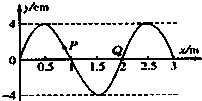 如图所示,是一列简谐横波在t=0时刻的波动图象.已知这列波沿x轴正方向传播,波速为5.0m/s.关于波上的P、Q两个质点的运动,以下说法正确的是( )
如图所示,是一列简谐横波在t=0时刻的波动图象.已知这列波沿x轴正方向传播,波速为5.0m/s.关于波上的P、Q两个质点的运动,以下说法正确的是( )
 如图所示,是一列简谐横波在t=0时刻的波动图象.已知这列波沿x轴正方向传播,波速为5.0m/s.关于波上的P、Q两个质点的运动,以下说法正确的是( )
如图所示,是一列简谐横波在t=0时刻的波动图象.已知这列波沿x轴正方向传播,波速为5.0m/s.关于波上的P、Q两个质点的运动,以下说法正确的是( )| A. | 在t=0时刻,质点P和Q的速度方向均沿y轴正方向 | |
| B. | P点和Q点振动的周期均为0.4s | |
| C. | 在t=0到t=0.1s的时间里,Q点的速度在不断增大 | |
| D. | 在t=0.1s到t=0.2s的时间里,Q点的加速度在不断减小 |
7.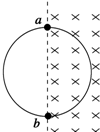 如图所示,用一根横截面积为S的硬导线做成一个半径为r的圆环,把圆环部分置于均匀变化的匀强磁场中,磁场方向垂直纸面向里,磁感应强度大小随时间的变化率$\frac{△B}{△t}$=k(k>0),ab为圆环的一条直径,导线的电阻率为ρ.则( )
如图所示,用一根横截面积为S的硬导线做成一个半径为r的圆环,把圆环部分置于均匀变化的匀强磁场中,磁场方向垂直纸面向里,磁感应强度大小随时间的变化率$\frac{△B}{△t}$=k(k>0),ab为圆环的一条直径,导线的电阻率为ρ.则( )
 如图所示,用一根横截面积为S的硬导线做成一个半径为r的圆环,把圆环部分置于均匀变化的匀强磁场中,磁场方向垂直纸面向里,磁感应强度大小随时间的变化率$\frac{△B}{△t}$=k(k>0),ab为圆环的一条直径,导线的电阻率为ρ.则( )
如图所示,用一根横截面积为S的硬导线做成一个半径为r的圆环,把圆环部分置于均匀变化的匀强磁场中,磁场方向垂直纸面向里,磁感应强度大小随时间的变化率$\frac{△B}{△t}$=k(k>0),ab为圆环的一条直径,导线的电阻率为ρ.则( )| A. | 圆环具有扩张的趋势 | B. | 图中ab两点间的电压大小为$\frac{1}{4}$kπr2 | ||
| C. | 圆环中感应电流的大小为$\frac{krs}{2ρ}$ | D. | 圆环中产生顺时针方向的感应电流 |
14.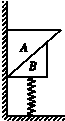 如图所示,两个三角形物块A、B叠放在竖直的轻弹簧上,靠着粗糙的竖直墙壁放置,用力F将物块竖直向下缓慢压一小段距离,然后又缓慢撤去力F,A、B恢复静止状态,整个过程中弹簧始终保持竖直,则力F撤去后( )
如图所示,两个三角形物块A、B叠放在竖直的轻弹簧上,靠着粗糙的竖直墙壁放置,用力F将物块竖直向下缓慢压一小段距离,然后又缓慢撤去力F,A、B恢复静止状态,整个过程中弹簧始终保持竖直,则力F撤去后( )
 如图所示,两个三角形物块A、B叠放在竖直的轻弹簧上,靠着粗糙的竖直墙壁放置,用力F将物块竖直向下缓慢压一小段距离,然后又缓慢撤去力F,A、B恢复静止状态,整个过程中弹簧始终保持竖直,则力F撤去后( )
如图所示,两个三角形物块A、B叠放在竖直的轻弹簧上,靠着粗糙的竖直墙壁放置,用力F将物块竖直向下缓慢压一小段距离,然后又缓慢撤去力F,A、B恢复静止状态,整个过程中弹簧始终保持竖直,则力F撤去后( )| A. | 弹簧的弹力大小大于两物块的总重力 | |
| B. | 墙壁对A有竖直向下的静摩擦力作用 | |
| C. | B对A的作用力大小大于A的重力大小 | |
| D. | A对B的静摩擦力沿接触面向下 |
11.第17届亚运会于2014年9月19日~10月4日在韩国仁川举行,我国运动员薛长锐、李玲以5.55m和4.35m分别夺得男、女撑杆跳金牌.如果把撑杆跳全过程分成四个阶段:a-b、b-c、c-d、d-e,如图所示,则对这四个阶段的下列描述正确的是( )
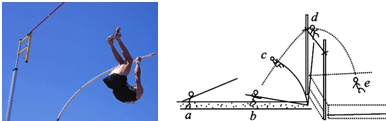

| A. | a-b阶段:加速助跑,人和杆的总机械能增加 | |
| B. | b-c阶段:杆弯曲、人上升,系统动能减少,重力势能和弹性势能增加 | |
| C. | c-d阶段:杆伸直、人上升,人的动能减少量等于重力势能增加量 | |
| D. | d-e阶段:人过横杆后下落,重力所做的功等于人机械能的增加量 |
9.一个物体从静止出发以加速度a做匀加速直线运动.经过时间t后,改作以t时刻末的速度做匀速直线运动,则在2t时间内的平均速度是( )
| A. | 3at | B. | $\frac{3}{4}$at | C. | $\frac{4}{3}$at | D. | $\frac{1}{2}$at |
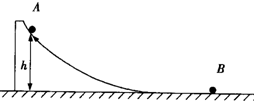 如图所示,一质量M=2kg的带有光滑弧形轨道的平台置于光滑且足够长的水平轨道上,弧形轨道与水平轨道平滑连接,水平轨道上静置一小球B.从弧形轨道上距离水平轨道高h=0.3m处由静止释放一质量mA=1kg的小球A,小球A沿轨道下滑后与小球B发生弹性正碰,碰后小球A被弹回,且恰好追不上平台.重力加速度为g.求小球B的质量.
如图所示,一质量M=2kg的带有光滑弧形轨道的平台置于光滑且足够长的水平轨道上,弧形轨道与水平轨道平滑连接,水平轨道上静置一小球B.从弧形轨道上距离水平轨道高h=0.3m处由静止释放一质量mA=1kg的小球A,小球A沿轨道下滑后与小球B发生弹性正碰,碰后小球A被弹回,且恰好追不上平台.重力加速度为g.求小球B的质量. 半径R=20cm的竖直放置的圆轨道与水平直轨道相连接,质量为m=50g的小球A以一定的初速度由直轨道向左运动,并沿圆轨道的内壁冲上去,如果球A经过N点时的速度v1=4m/s,A经过M点时对轨道的压力为0.5N.取g=10m/s2,求:
半径R=20cm的竖直放置的圆轨道与水平直轨道相连接,质量为m=50g的小球A以一定的初速度由直轨道向左运动,并沿圆轨道的内壁冲上去,如果球A经过N点时的速度v1=4m/s,A经过M点时对轨道的压力为0.5N.取g=10m/s2,求: