题目内容
9.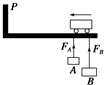 如图,天车下吊着两个质量都是m的工件A和B,整体一起向左匀速运动.系A的吊绳较短,系B的吊绳较长,若天车运动到P处时突然停止,则两吊绳所受拉力FA、FB的大小关系是( )
如图,天车下吊着两个质量都是m的工件A和B,整体一起向左匀速运动.系A的吊绳较短,系B的吊绳较长,若天车运动到P处时突然停止,则两吊绳所受拉力FA、FB的大小关系是( )| A. | FA>FB>mg | B. | FA<FB<mg | C. | FA=FB=mg | D. | Fa=FB>mg |
分析 天车运动到P处突然停止时,A、B由于惯性,要继续运动,将做圆周运动,根据径向的合力提供向心力,求出拉力,从而比较出FA、FB的大小关系.
解答 解:天车运动到P处突然停止时,A、B以相同的速度将做圆周运动,根据F-$mg=m\frac{{v}^{2}}{L}$得:F=mg+$\frac{m{v}^{2}}{L}$,因为A的绳长小于B的绳长,则A的拉力大于B的拉力.故A正确,B、C、D错误.
故选:A
点评 解决本题的关键能够判断出天车突然停止时A、B的运动情况,以及知道圆周运动径向的合力提供向心力.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
19.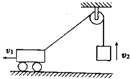 如图所示,在水平地面上做匀速直线运动的小车,通过定滑轮用绳子吊起一个物体,若小车和被吊的物体在同一时刻的速度分别为v1和v2,绳子对物体的拉力为FT,物体所受重力为G,则下列说法正确的是( )
如图所示,在水平地面上做匀速直线运动的小车,通过定滑轮用绳子吊起一个物体,若小车和被吊的物体在同一时刻的速度分别为v1和v2,绳子对物体的拉力为FT,物体所受重力为G,则下列说法正确的是( )
 如图所示,在水平地面上做匀速直线运动的小车,通过定滑轮用绳子吊起一个物体,若小车和被吊的物体在同一时刻的速度分别为v1和v2,绳子对物体的拉力为FT,物体所受重力为G,则下列说法正确的是( )
如图所示,在水平地面上做匀速直线运动的小车,通过定滑轮用绳子吊起一个物体,若小车和被吊的物体在同一时刻的速度分别为v1和v2,绳子对物体的拉力为FT,物体所受重力为G,则下列说法正确的是( )| A. | 物体做匀速直线运动,且v1=v2 | B. | 物体做加速直线运动,且v2>v1 | ||
| C. | 物体做加速直线运动,且FT>G | D. | 物体做匀速直线运动,且FT=G |
17.一小球被细绳拴着,在水平面内做半径为R的匀速圆周运动,向心加速度为a,那么说法中不正确的是( )
| A. | 小球的角速度为ω=$\sqrt{\frac{a}{R}}$ | |
| B. | 小球在时间t内通过的路程s=t$\sqrt{aR}$ | |
| C. | 小球做匀速圆周运动的周期T=$\sqrt{\frac{a}{R}}$ | |
| D. | 小球在时间t内可能发生的最大位移为2R |
4.在绕轨道飞行的人造地球卫星上的开口容器中装有某种液体,若该液体在地球上是可浸润器壁的,则( )
| A. | 在卫星上该液体不再浸润器壁 | |
| B. | 在卫星上该液体仍可浸润器壁 | |
| C. | 在卫星上该液体将沿器壁流到容器外去 | |
| D. | 在卫星上该液体仍保留与在地面时相同的形状 |
1.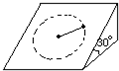 如图所示,在倾角为30°的光滑绝缘斜面上有一质量为m、带电量为+q的小球,小球被一绝缘细线系于斜面上的O点,为了使它能在斜面上做匀速圆周运动,可以加一个匀强电场,该电场的方向和大小可能是( )
如图所示,在倾角为30°的光滑绝缘斜面上有一质量为m、带电量为+q的小球,小球被一绝缘细线系于斜面上的O点,为了使它能在斜面上做匀速圆周运动,可以加一个匀强电场,该电场的方向和大小可能是( )
 如图所示,在倾角为30°的光滑绝缘斜面上有一质量为m、带电量为+q的小球,小球被一绝缘细线系于斜面上的O点,为了使它能在斜面上做匀速圆周运动,可以加一个匀强电场,该电场的方向和大小可能是( )
如图所示,在倾角为30°的光滑绝缘斜面上有一质量为m、带电量为+q的小球,小球被一绝缘细线系于斜面上的O点,为了使它能在斜面上做匀速圆周运动,可以加一个匀强电场,该电场的方向和大小可能是( )| A. | 方向与斜面成30°角向下,大小为$\frac{mgtan30°}{q}$ | |
| B. | 方向沿斜面向上,大小为$\frac{mgsin30°}{q}$ | |
| C. | 方向垂直斜面向下,大小为$\frac{mgsin30°}{q}$ | |
| D. | 方向竖直向下,大小为$\frac{mg}{q}$ |
19.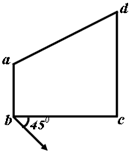 如图所示,a、b、c、d为某匀强电场中的四个点,且ab∥cd、ab⊥bc,bc=cd=2ab=2l,电场线与四边形所在平面平行.已知φa=20V,φb=24V,φd=8V.一个质子经过b点的速度大小为v0,方向与bc夹角为45°,一段时间后经过c点,不计质子的重力,则( )
如图所示,a、b、c、d为某匀强电场中的四个点,且ab∥cd、ab⊥bc,bc=cd=2ab=2l,电场线与四边形所在平面平行.已知φa=20V,φb=24V,φd=8V.一个质子经过b点的速度大小为v0,方向与bc夹角为45°,一段时间后经过c点,不计质子的重力,则( )
 如图所示,a、b、c、d为某匀强电场中的四个点,且ab∥cd、ab⊥bc,bc=cd=2ab=2l,电场线与四边形所在平面平行.已知φa=20V,φb=24V,φd=8V.一个质子经过b点的速度大小为v0,方向与bc夹角为45°,一段时间后经过c点,不计质子的重力,则( )
如图所示,a、b、c、d为某匀强电场中的四个点,且ab∥cd、ab⊥bc,bc=cd=2ab=2l,电场线与四边形所在平面平行.已知φa=20V,φb=24V,φd=8V.一个质子经过b点的速度大小为v0,方向与bc夹角为45°,一段时间后经过c点,不计质子的重力,则( )| A. | c点电势为16V | |
| B. | 场强的方向由a指向d | |
| C. | 质子从b运动到c所用的时间为$\frac{\sqrt{2}l}{{v}_{0}}$ | |
| D. | 质子运动到c时的速度大小为$\sqrt{2}$v0 |
 如图所示,从A点以v0的水平速度抛出一质量m=1kg的小物块(可视为质点),当小物块运动至B点时,恰好沿切线方向进入固定的光滑圆弧轨道BC,圆弧轨道BC的圆心角α=37°经圆孤轨道后滑上与C点等高、静止在粗糙水平面的长木板上,圆弧轨道C端切线水平.已知长木板的质量M=4kg,A、B两点距C点的高度分别为H=0.6m、h=0.15m,小物块与长木板之间的动摩擦因数μ1=0.5,长木板与地面间的动摩擦因数μ2=0.2,cos37°=0.8,sin37°=0.6,g=10m/s2.求:
如图所示,从A点以v0的水平速度抛出一质量m=1kg的小物块(可视为质点),当小物块运动至B点时,恰好沿切线方向进入固定的光滑圆弧轨道BC,圆弧轨道BC的圆心角α=37°经圆孤轨道后滑上与C点等高、静止在粗糙水平面的长木板上,圆弧轨道C端切线水平.已知长木板的质量M=4kg,A、B两点距C点的高度分别为H=0.6m、h=0.15m,小物块与长木板之间的动摩擦因数μ1=0.5,长木板与地面间的动摩擦因数μ2=0.2,cos37°=0.8,sin37°=0.6,g=10m/s2.求: