题目内容
在平直的轨道上,甲、乙两车相距为s,同向同时开始运动.甲在后以初速度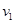 ,加速度
,加速度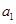 做匀加速运动,乙在前作初速度为零,加速度为
做匀加速运动,乙在前作初速度为零,加速度为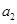 的匀加速运动.假定甲能从乙的旁边通过而互不影响,下列情况可能发生的是
的匀加速运动.假定甲能从乙的旁边通过而互不影响,下列情况可能发生的是
A.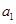 = =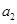 时,甲、乙只能相遇一次 时,甲、乙只能相遇一次 |
B.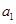 > >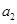 时,甲、乙可能相遇二次 时,甲、乙可能相遇二次 |
C.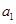 > >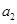 时,甲、乙只能相遇一次 时,甲、乙只能相遇一次 |
D.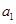 < <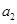 时,甲、乙可能相遇二次 时,甲、乙可能相遇二次 |
ACD
解析试题解析:对于A而言,a1=a2,由公式v=v0+at知:甲的速度始终大于乙的速度,甲追上乙相遇之后,甲在前速度比乙大,距离越来越远,故不可能再次相遇,所以甲乙只能相遇一次,故A正确;
对于B而言,当a1大于a2时,由公式v=v0+at知:甲的速度始终大于乙的速度,甲追上乙相遇之后,甲在前速度比乙大,距离越来越远.不可能再次相遇.所以甲乙只能相遇一次,故B错误,C正确;
对于D而言,当a1小于a2时,由公式v=v0+at知,甲的速度先是大于乙的,由于乙的加速度是大于甲的,一定时间之后,乙的速度会等于甲的速度,再继续乙的速度就大于甲的速度,通过速度关系可以想到,甲、乙的距离先是减小,以下可能分几种情况:
①当甲乙的速度达到相等时,甲还没有追上乙,之后就别想追上了,也就是不能相遇;
②当甲乙的速度达到相等时,甲正好这时相遇乙,之后两者距离越来越大,也就是相遇一次;
③当甲乙的速度达到相等之前,甲追上相遇乙,之后甲在前,乙在后,变成乙追甲,两者速度相等之后乙的速度就大于甲的,乙就会追上甲再相遇一次,也就是一共相遇了两次,故D正确。
故选ACD是正确的。
考点:匀变速直线运动的追击与相遇问题。

 阅读快车系列答案
阅读快车系列答案如图所示,以8m/s匀速行驶的汽车即将通过路口,绿灯还有2 s将熄灭,此时汽车距离停车线18m。该车加速时最大加速度大小为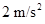 ,减速时最大加速度大小为
,减速时最大加速度大小为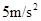 。此路段允许行驶的最大速度为
。此路段允许行驶的最大速度为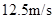 ,下列说法中正确的有( )
,下列说法中正确的有( )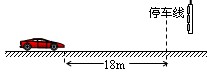
| A.如果立即做匀加速运动,在绿灯熄灭前汽车可能通过停车线 |
| B.如果立即做匀加速运动,在绿灯熄灭前通过停车线汽车一定超速 |
| C.如果立即做匀减速运动,在绿灯熄灭前汽车一定不能通过停车线 |
D.如果距停车线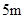 处减速,汽车能停在停车线处 处减速,汽车能停在停车线处 |
如图所示,几条足够长的光滑直轨道与水平面成不同角度,从P点以大小不同的初速度沿各轨道发射小球,若各小球恰好在相同的时间内达到各自的最高点,则各小球最高点的位置
| A.在同一水平线上 | B.在同一竖直线上 |
| C.在同一抛物线上 | D.在同一圆周上 |
几个做匀变速直线运动的物体,在时间t内位移一定最大的是( )
| A.平均速度最大的物体 | B.初速度最大的物体 |
| C.末速度最大的物体 | D.加速度最大的物体 |
如图所示,由电动机带动的水平传送带以速度为v=2.0m/s匀速运行,A端上方靠近传送带料斗中装有煤,打开阀门,煤以流量为Q=50kg/s落到传送带上,煤与传送带达共同速度后被运至B端,在运送煤的过程中,下列说法正确的是( )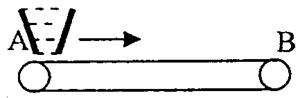
| A.电动机应增加的功率为100W |
| B.电动机应增加的功率为200W |
| C.在一分钟内因煤与传送带摩擦产生的热为6.0×103J |
| D.在一分钟内因煤与传送带摩擦产生的热为1.2×104J |
如图所示,一名消防队员在模拟演习训练中,沿着长为12m的竖立在地面上的钢管下滑。已知这名消防队员的质量为60kg,他从钢管顶端由静止开始先匀加速再匀减速下滑,滑到地面时速度恰好为零。如果他加速时的加速度大小是减速时的2倍,下滑的总时间为3s,g取10m/s2,那么该消防队员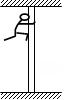
| A.下滑过程中的最大速度为4m/s |
| B.加速与减速过程的时间之比为2:1 |
| C.加速与减速过程中所受摩擦力大小之比为1∶7 |
| D.加速与减速过程的位移之比为1∶4 |
如图所示,以8m/s匀速行驶的汽车即将通过路口,绿灯还有2 s将熄灭,此时汽车距离停车线18m。该车加速时最大加速度大小为 2m/s2,减速时最大加速度大小为 5m/s2。此路段允许行驶的最大速度为12.5m/s ,下列说法中正确的有( )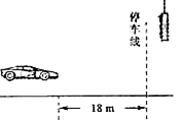
| A.如果立即做匀加速运动,在绿灯熄灭前汽车可能通过停车线 |
| B.如果立即做匀加速运动,在绿灯熄灭前通过停车线汽车一定超速 |
| C.如果立即做匀减速运动,在绿灯熄灭前汽车一定不能通过停车线 |
| D.如果距停车线 5m处减速,汽车能停在停车线处 |