题目内容
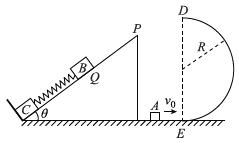
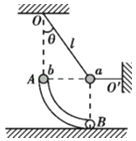
【题目】如图所示，倾角为θ的倾斜平行直轨道与竖直面内的平行圆形轨道平滑对接，轨道之间距离为L，圆形轨道的半径为r，在倾斜平行轨道上半部分处有磁感应强度为B的垂直于轨道平面的匀强磁场，磁场区域足够大，圆形轨道末端接有一阻值为R的电阻。质量分布均匀且为m的金属棒a从距轨道最低点C高度为H处静止释放，运动到最低点C时的速度大小
，恰好与放在此处质量分布均匀的金属棒b发生碰撞，碰后粘在一起。金属棒a、b电阻都是R且直径相对圆形轨道半径r忽略不计，轨道电阻不计，不计一切摩擦，求：
（1）金属棒中产生感应电动势的最大值Em；
（2）金属棒下滑过程中整个电路产生的热量Q；
（3）若碰后金属棒a、b不脱离轨道，求金属棒b的质量的取值范围。
【答案】（1）
（2）mgH-5mgr；（3）
或者
【解析】
（1）从金属棒刚离开磁场到到达C点过程中，由机械能守恒定律得：
最大感应电动势：
Em=BLv
解得：
；
（2）金属棒从静止开始运动到C点过程中，由能量守恒定律得：
解得：
Q=mgH-5mgr；
（3）金属棒ab碰后，由动量守恒：
情况1:若两棒上升的高度小于圆环轨道的半径r时，则：
解得：
情况2:若两棒恰能上升到圆环轨道最高点，则：
解得：
则要想碰后金属棒a、b不脱离轨道，金属棒b的质量的取值范围：
或者
练习册系列答案
相关题目
