题目内容
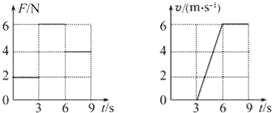
【题目】如图所示，固定在水平面上倾角
的光滑斜面底端有一垂直于斜面的挡板，可看成质点的物块A、B、C质量均为m=2.5kg，物块B、C通过一劲度系数k=72N/m的轻质弹簧相连，初始时，物块C靠在挡板上，物块B、C处于静止状态，物块A以初速度v0沿光滑的水平面进入竖直面内与水平面相切于E点、半径R=1.2m的光滑固定半圆形轨道。当物块A到达轨道的最高点D时，对轨道的压力大小为
，物块A离开D点后，恰好无碰撞地由P点滑上斜面，继续运动
后与静止于Q点的物块B相碰，碰撞时间极短，碰后物块A、B粘在一起，已知不计空气阻力，重力加速度g=10m/s2，sin37°=0.6，cos37°=0.8。求：
（1）物块A的初速度v0的大小；
（2）物块A、B碰撞后瞬间的共同速度v的大小；
（3）设从物块A、B粘在一起到物块C恰好离开挡板这一过程经历了时间t，若t=1s，则这一过程中弹簧对物块C的冲量大小I为多少？（弹簧始终处于弹性限度内）
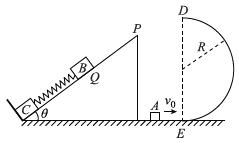
【答案】（1）
（2）
（3）
【解析】
（1）当物块A到达D点时，对物块A受力分析有
，解得
物块A从开始运动到D点的过程中，由动能定理得
解得
（2）当物块A离开D点后，物块A做平抛运动，到达P点时速度沿斜面向下
则
从P点到Q点的过程中，由动能定理得
解得
从物块A与物块B相碰到碰撞结束这一过程，由动量守恒定律得
解得
（3）设在碰撞前弹簧的压缩量为x1，受力分析得
kx1=mgsin37°，可得
当物块C恰好离开挡板时，弹簧处于伸长状态，设伸长量为x2，对物块C受力分析得
，可得
从物块A、B碰撞完到物块C恰好离开挡板，设此时物块A、B的共同速度为v1，以物块A、B为研究对象，此过程弹簧的弹力做功为零，由动能定理得
解得
从物块A、B碰撞完到物块C恰好离开挡板，设弹簧对物块A、B的冲量为
，规定沿斜面向上为正方向，由动量定理得
此过程弹簧对物块C的冲量大小
