Question

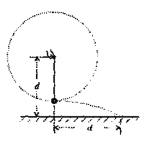
【题目】某学习小组要验证机械能守恒定律，实验装置如图1所示，细线端拴一个球，另一端连接力传感器，固定在天花板上，传感器可记录球在摆动过程中细线拉力大小，用量角器量出释放球时细线与竖直方向的夹角，用天平测出球的质量为m。重力加速度为g。

（1）用游标卡尺测出小球直径如图2所示，读数为_____mm；

（2）将球拉至图示位置，细线与竖直方向夹角为θ，静止释放球，发现细线拉力在球摆动过程中作周期性变化。为求出球在最低点的速度大小，应读取拉力的_____（选填“最大值”或“最小值”），其值为F。

（3）球从静止释放运动到最低点过程中，满足机械能守恒的关系式为_____（用测定物理量的符号表示）。

Answer 1

【答案】18.50 最大值 2mg（1﹣cosθ）＝F﹣mg

【解析】

（1）[1]．小球的直径：d=18mm+10×0.05mm=18.50mm

（2）[2]．球在最低点的速度最大，对应的拉力最大，为求出球在最低点的速度大小，应读取拉力的最大值。

（3）[3]．在最低点：

球从静止释放运动到最低点过程中，满足机械能守的关系式：

解得：

2mg（1-cosθ）=F-mg