题目内容
【题目】航模兴趣小组设计出一架遥控飞行器，其质量m=2kg，动力系统提供的恒定升力F=28N．试飞时，飞行器从地面由静止开始竖直上升．设飞行器飞行时所受的阻力大小不变，g取10m/s2 ．
（1）第一次试飞，飞行器飞行t1=8s 时到达高度H=64m．求飞行器所阻力f的大小；
（2）第二次试飞，飞行器飞行t2=6s 时遥控器出现故障，飞行器立即失去升力．求飞行器能达到的最大高度h；
（3）为了使飞行器不致坠落到地面，求飞行器从开始下落到恢复升力的最长时间t3 ．
【答案】
（1）
解：第一次飞行中，设加速度为a1
匀加速运动 
由牛顿第二定律F﹣mg﹣f=ma1
解得f=4N
（2）
解：第二次飞行中，设失去升力时的速度为v1，上升的高度为s1
匀加速运动 
设失去升力后的加速度为a2，上升的高度为s2
由牛顿第二定律mg+f=ma2v1=a1t2 
解得h=s1+s2=42m
（3）
解：设失去升力下降阶段加速度为a3；恢复升力后加速度为a4，恢复升力时速度为v3
由牛顿第二定律 mg﹣f=ma3
F+f﹣mg=ma4
且 
V3=a3t3
解得t3= 
s（或2.1s）
【解析】（1）第一次试飞时，飞行器从地面由静止开始竖直上升做匀加速直线运动，根据位移时间公式可求出加速度，再根据牛顿第二定律就可以求出阻力f的大小；（2）失去升力飞行器受重力和阻力作用做匀减速直线运动，当速度减为0时，高度最高，等于失去升力前的位移加上失去升力后的位移之和；（3）求飞行器从开始下落时做匀加速直线运动，恢复升力后做匀减速直线运动，为了使飞行器不致坠落到地面，到达地面时速度恰好为0，根据牛顿第二定律以及运动学基本公式即可求得飞行器从开始下落到恢复升力的最长时间t3 ．
阅读快车系列答案【题目】某同学在做“利用单摆测重力加速度”的实验中，先测得摆线长为97.50 cm，摆球直径为2.00 cm，然后用秒表记录了单摆振动50次所用的时间，如图所示，则：
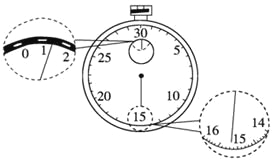
(1)该摆摆长为______cm，秒表所示读数为______s.
(2)如果测得的g值偏小，可能的原因是( )
A．测摆线长时摆线拉得过紧 |
B．摆线上端悬点未固定，振动中出现松动，使摆线长度增加了 |
C．开始计时时，秒表过迟按下 |
D．实验中误将49次全振动记为50次 |
(3)为了提高实验精度，在实验中可改变几次摆长l并测出相应的周期T，从而得出一组对应的l与T的数据，再以l为横坐标，T2为纵坐标，将所得数据连成直线如图所示，并求得该直线的斜率为k，则重力加速度g＝______(用k表示)．
