��Ŀ����
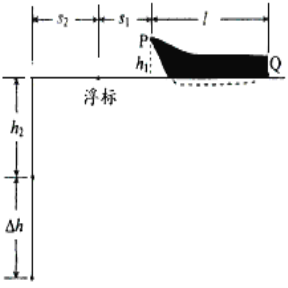
����Ŀ���ļ���һ��Ⱦ����ִ̼����˶������������˵�ϲ������ͼ��ʾ��ԭ��L=16m����Ƥ��һ�˹̶������ܵ�P�㣬��һ��ϵ�ڱļ��ߵ��������ļ��ߴ�P���ɾ�ֹ���£�����A��ʱ���պ���ֱ�������½�����͵�B����BP֮�����h=20m����֪���ļ��ߵ�����m=60kg�����ܿ�������f��Ϊ���ص� ![]() ���ļ��߿���Ϊ�ʵ㣬g=10m/s2 �� ��
���ļ��߿���Ϊ�ʵ㣬g=10m/s2 �� ��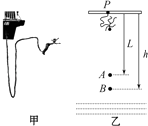
��1���ļ��ߵ���A��ʱ���ٶȣ�
��2����Ƥ���ĵ������ܵ����ֵ��
��3���ļ��ߴ�P�½���A���ٴ�A�½���B��е�ܵı仯���ֱ��Ϊ��E1����E2 �� ���E1����E2Ϊ���٣�
���𰸡�
��1��
�⣺�Աļ��ߴ�P��A�����ɶ��ܶ����ã�
mgL��fL= ![]() ��
��
����f= ![]() mg��
mg��
�������ݽ�ã� ![]() =16m/s
=16m/s
��2��
�⣺�Աļ����뵯����ɵ�ϵͳ��P��B�����������غ㶨�ɿɵã�
mgh=fh+ ![]() ��
��
��ã� ![]() =��mg��f��h=9600J
=��mg��f��h=9600J
��3��
�⣺���ݡ�����ԭ������֪����P�½���A�����У���е�ܼ���Ϊ�� ![]() =fL��
=fL��
��A�½���B�����л�е�ܼ���Ϊ�� ![]() =f��h��L��
=f��h��L��
�����ɵã� ![]() =
= ![]()
�����������⣨1���Ĺؼ��ǶԱļ���Ӧ�ö��ܶ������ɣ��⣨2���Ĺؼ��ǶԱļ����뵯����ɵ�ϵͳӦ�������غ㶨�ɼ�����⣻�⣨3���Ĺؼ�����ȷ���ݹ���ԭ������е�ܵı仯��
�����㾫�������ն��ܶ������ۺ�Ӧ���ǽ����ĸ�������Ҫ֪��Ӧ�ö��ܶ���ֻ���dz���ĩ״̬��û���غ����������ƣ�Ҳ�����������ʺ��������̵ı仯��Ӱ��.���ԣ����漰����λ�ƣ������漰��������ʱ��Ķ���ѧ���⣬�������ö��ܶ��������ͽ�𣬶���һ�㶼����ţ���˶����ɺͻ�е���غ㶨�ɼ�ݣ�

 ������ϵ�д�
������ϵ�д�