题目内容
15.一平直铁路与旁边一条公路平行,正当列车以20m/s的初速度前进并以-0.1m/s2的加速度刹车时,前方155m处的自行车正以4m/s的速度匀速向同一方向运动,试判断列车会不会追上自行车,如果追不上,求两车相距最近时的距离;如果追上,从刹车时开始计时,求列车与自行车相遇的时间.分析 火车追上自行车时火车的位移等于自行车的位移+两者间距离,根据各自位移时间关系求解即可;
解答 解:假设火车能追上自行车,火车的位移等于自行车的位移加上两车间的距离,故由题意有:
${x}_{火}={v}_{0}t+\frac{1}{2}a{t}^{2}$=20t-0.05t2
x自=v自t
当他们相遇时有:x火=x自+155;即:
20t-0.05t2=4t+155
解得:t1=10s,t2=310s(舍去);
因为火车的初速度为20m/s,加速度为a=-0.1m/s2可得火车停车时间为200s,故能追上
所需时间为10s
答:能追上,所需时间为10s
点评 本题抓住追及相遇问题的位移特征展开讨论,即位移再次相等时相遇或超过

练习册系列答案
相关题目
5.有一个小球从距地面某高度处竖直向上抛出,运动过程受空气阻力作用,以下说法正确的是( )
| A. | 小球上升到最高点时重力势能最大 | |
| B. | 小球上升到最高点时机械能最大 | |
| C. | 小球从抛出到落地整个过程中,合力的功可能为0 | |
| D. | 小球从抛出到落地整个过程中,合力一定做正功 |
6. 如图所示,一定质量的理想气体,经过图线A→B→C→A的状态变化过程,AB的延长线过O点,CA与纵轴平行.由图线可知( )
如图所示,一定质量的理想气体,经过图线A→B→C→A的状态变化过程,AB的延长线过O点,CA与纵轴平行.由图线可知( )
 如图所示,一定质量的理想气体,经过图线A→B→C→A的状态变化过程,AB的延长线过O点,CA与纵轴平行.由图线可知( )
如图所示,一定质量的理想气体,经过图线A→B→C→A的状态变化过程,AB的延长线过O点,CA与纵轴平行.由图线可知( )| A. | A→B过程压强不变,外界对气体做功 | B. | B→C过程压强增大,外界对气体做功 | ||
| C. | C→A过程压强不变,外界对气体做功 | D. | C→A过程压强减小,气体对外界做功 |
3.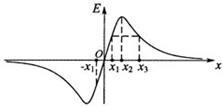 等量同种点电荷连线中垂线上的电场强度E随x变化的图象如图所示.下列说法正确的是( )
等量同种点电荷连线中垂线上的电场强度E随x变化的图象如图所示.下列说法正确的是( )
 等量同种点电荷连线中垂线上的电场强度E随x变化的图象如图所示.下列说法正确的是( )
等量同种点电荷连线中垂线上的电场强度E随x变化的图象如图所示.下列说法正确的是( )| A. | O点的电势最高 | |
| B. | x2点的电势为零 | |
| C. | x1与x2两点间的电势差小于x2与x3两点间的电势差 | |
| D. | x1点的电势比-x1点的电势高 |
20.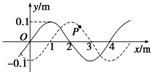 一列简谐横波沿x轴正方向传播,t=0时刻的波形如图中实线所示,t=0.1s时刻的波形如图中虚线所示.波源不在坐标原点O,P是传播介质中离坐标原点xp=2.5m处的一个质点.则以下说法正确的是( )
一列简谐横波沿x轴正方向传播,t=0时刻的波形如图中实线所示,t=0.1s时刻的波形如图中虚线所示.波源不在坐标原点O,P是传播介质中离坐标原点xp=2.5m处的一个质点.则以下说法正确的是( )
 一列简谐横波沿x轴正方向传播,t=0时刻的波形如图中实线所示,t=0.1s时刻的波形如图中虚线所示.波源不在坐标原点O,P是传播介质中离坐标原点xp=2.5m处的一个质点.则以下说法正确的是( )
一列简谐横波沿x轴正方向传播,t=0时刻的波形如图中实线所示,t=0.1s时刻的波形如图中虚线所示.波源不在坐标原点O,P是传播介质中离坐标原点xp=2.5m处的一个质点.则以下说法正确的是( )| A. | 质点P的振幅为0.1 m | |
| B. | 波的频率可能为7.5 Hz | |
| C. | 波的传播速度可能为50 m/s | |
| D. | 在t=0.1 s时刻与P相距5 m处的质点一定沿x轴正方向运动 | |
| E. | 在t=0.1 s时刻与P相距5 m处的质点可能是向上振动,也可能是向下振动 |
7. 如图中虚线为匀强电场中的等势线,两粒子M、N质量相等,所带电荷的绝对值也相等.现将M、N从虚线上的O点以相同速率射出,两粒子在电场中运动的轨迹分别如图中两条实线所示.点a、b、c为实线与虚线的交点,已知O点电势高于c点.若不计重力,则( )
如图中虚线为匀强电场中的等势线,两粒子M、N质量相等,所带电荷的绝对值也相等.现将M、N从虚线上的O点以相同速率射出,两粒子在电场中运动的轨迹分别如图中两条实线所示.点a、b、c为实线与虚线的交点,已知O点电势高于c点.若不计重力,则( )
 如图中虚线为匀强电场中的等势线,两粒子M、N质量相等,所带电荷的绝对值也相等.现将M、N从虚线上的O点以相同速率射出,两粒子在电场中运动的轨迹分别如图中两条实线所示.点a、b、c为实线与虚线的交点,已知O点电势高于c点.若不计重力,则( )
如图中虚线为匀强电场中的等势线,两粒子M、N质量相等,所带电荷的绝对值也相等.现将M、N从虚线上的O点以相同速率射出,两粒子在电场中运动的轨迹分别如图中两条实线所示.点a、b、c为实线与虚线的交点,已知O点电势高于c点.若不计重力,则( )| A. | M带负电荷,N带正电荷 | |
| B. | M带正电荷,N带负电荷 | |
| C. | N在从O点运动至a点的过程中电势降低 | |
| D. | M在O点和b点电势能相同 |
 在如图所示的电路中,电阻R1=6Ω,R2=3Ω,电压表视为理想电表.当开关S断开时,电压表示数为9V,当开关S闭合时,电压表示数为6V.求:
在如图所示的电路中,电阻R1=6Ω,R2=3Ω,电压表视为理想电表.当开关S断开时,电压表示数为9V,当开关S闭合时,电压表示数为6V.求: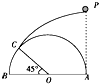 如图所示,半径为R的半圆柱体置于水平地面上,在其右端点A点的正上方P处有一可视为质点的小球.小球以某一初速度水平向左抛出,其运动轨迹恰好与半圆柱体相切于C点,∠COB=45°,重力加速度为g,则小球从P点运动到C点时的水平位移为(1+$\frac{\sqrt{2}}{2}$)R,时间为$\sqrt{\frac{(1+\frac{\sqrt{2}}{2})R}{g}}$.
如图所示,半径为R的半圆柱体置于水平地面上,在其右端点A点的正上方P处有一可视为质点的小球.小球以某一初速度水平向左抛出,其运动轨迹恰好与半圆柱体相切于C点,∠COB=45°,重力加速度为g,则小球从P点运动到C点时的水平位移为(1+$\frac{\sqrt{2}}{2}$)R,时间为$\sqrt{\frac{(1+\frac{\sqrt{2}}{2})R}{g}}$.