Question

【题目】在“探究加速度与力、质量的关系”实验中：

(1)以下实验操作，正确的是________

A.平衡摩擦力时，应将空砝码盘用细线跨过定滑轮系在小车上，让细线与长木板平行

B.平衡摩擦力时，应将纸带连接在小车上并穿过打点计时器

C.每次改变小车质量时，不需要重新平衡摩擦力

D.实验时，应先释放小车，再接通电源

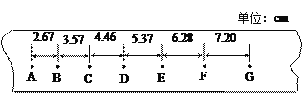
(2)下图是实验中得到的一条已打点的纸带，纸带上的A、B、C、D、E、F、G均为相邻计数点，已知打点计时器的打点周期为0.02s，相邻两个计数点之间还有4个计时点未画出，相邻计数点之间的距离已标注在图上，则小车运动的加速度大小a=______m/s2，打C点时的速度大小vC=________m/s。（以上结果都保留2位有效数字）。

Answer 1

【答案】BC；0.91；0.40

【解析】

(1)A项：平衡摩擦力时，应将绳从小车上拿去，轻轻推动小车，小车沿木板运动，通过打点计时器打出来的纸带判断小车是否匀速运动,故A错误；

B项：平衡摩擦力时，应将纸带连接在小车上并穿过打点计时器，故B正确；

C项：每次改变小车的质量时，小车的重力沿斜面分力和摩擦力仍能抵消，不需要重新平衡摩擦力，故C正确；

D项：实验时，如果先放开小车，再接通打点计时器电源，由于小车运动较快，可能会使打出来的点很少，不利于数据的采集和处理，所以应该先接通电源，再放开小车，故D错误。

故选BC。

(2) 由于每相邻两个计数点间还有4个点没有画出，所以相邻的计数点间的时间间隔T=0.1s，

根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小，得：

x4-x1=3a1T2

x5-x2=3a2T2

x6-x3=3a3T2

为了更加准确的求解加速度，我们对三个加速度取平均值，得：

即小车运动的加速度为：

根据匀变速直线运动中时间中点的速度等于该过程中的平均速度，可以求出打纸带上C点时小车的瞬时速度大小：

。