题目内容
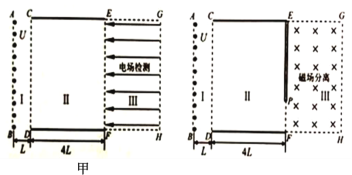
【题目】如图所示，质量为m、长度为L的滑板B，静置于水平面上，滑板与地面间的动摩擦因数μ1=μ，水平面右端的固定挡板C与滑板等高。在挡板C的右边有一个区域PQMM，区域内有竖直向上的匀强电场，还有两个半径分别为R1=r和R2=3r的半圆构成的半圆环区域，在半圆环区域内有垂直纸面向里的匀强磁场，半圆环圆心O到固定挡板C顶点的距离为2r。现有一质量为m带电量为+q的小物块A(视为质点)以初速度v0=2
滑上滑板B，A与B之间的动摩擦因数μ2=3μ。当小物块A运动到滑板B右端时两者刚好共速，且滑板B刚好与挡板C碰撞，A从挡板C上方飞入PQNM区城，并能够在半圆环磁场区域内做匀速圆周运动。求：
(1)A刚滑上B时，A和B的加速度大小；
(2)A刚滑上B时，B右端与挡板C之间的距离S；
(3)区域PQMN内电场强度E的大小，以及要保证小物块A只能从半圆环区域的开口端飞出，磁感应强度B的取值范围。
【答案】（1）μg；3μg（2）L/4（3）
；
或 
【解析】
（2）根据牛顿第二定律求解A刚滑上B时，A和B的加速度大小；（2）由运动公式求解A刚滑上B时，B右端与挡板C之间的距离S；（3）A进入区域PQNM，并能在半圆环磁场区域内做匀速圆周运动，则电场力和重力平衡，洛伦兹力充当向心力；结合几何关系，求解保证小物块A只能从半圆环区域的开口端飞出，磁感应强度B的取值范围.
（1）对物块A有：
解得a2=μ2g=3μg；
对滑块B：
解得：a1=μ2g-2μ1g=μg
（2）设AB的共同速度为v，
对小物块A：
对B: 
解得
（3）A进入区域PQNM，并能在半圆环磁场区域内做匀速圆周运动，则：mg=qE
解得
粒子做匀速圆周运动：
要使物块A不从半圆环区域的内环和外环飞出磁场要满足：
；解得
，即
②
；解得
；即
综上，要让物块A不从半圆环区域的内环和外环飞出磁场B要满足：
或
