Question

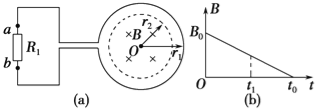
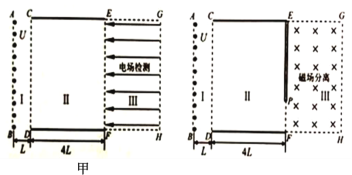
【题目】现在很多家庭或者单位刚装修结束，都要进行空气检测和治理．某环保设备装置可用于气体中有害离子的检测和分离．离子检测的简化原理如图所示．Ⅰ区为电场加速区，Ⅱ区为无场区，Ⅲ区为电场检测区．已知Ⅰ区中AB与CD两极的电势差为U，距离为L，Ⅱ区中CE与DF两板的间距为d，板长为4L，Ⅲ区中EF与GH间距足够大，其内部匀强电场的电场强度为，方向水平向左．假设大量相同的正离子在AB极均匀分布，由初速度为零开始加速，不考虑离子间的相互作用和重力影响，则：

(1)AB与CD哪一极电势高？若正离子的比荷为k，求该离子到达CD极时的速度大小；

(2)该装置可以测出离子从AB极出发，经过Ⅰ区、Ⅱ区和Ⅲ区，最后返回EF端的总时间为t，由此可以确定离子的比荷为k，试写出k与t的函数关系式；

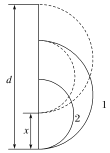
(3)若将Ⅲ区的匀强电场换成如图所示的匀强磁场，则电场检测区变成了磁场分离区，为收集分离出的离子，需在EF边上放置收集板EP，收集板下端留有狭缝PF，离子只能通过狭缝进入磁场进行分离．假设在AB极上有两种正离子，质量分别为m、M，且1<≤4，电荷量均为Q，现要将两种离子在收集板上完全分离，同时为收集更多离子，狭缝尽可能大，试讨论狭缝PF宽度的最大值与m、M、d的关系式．(磁感应强度大小可调，不考虑出Ⅲ区后再次返回的离子)

Answer 1

【答案】（1） （2） （3）

【解析】

（1）正离子在电极AB和CD间做加速运动，电场方向水平向右，所以AB电极带正电，根据动能定理求离子到达CD电极的速度；

（2）由运动学公式分别求出离子在Ⅰ区、Ⅱ区、Ⅲ区的运动时间，求出总时间即可得到k与m的关系式；

（3）两种离子从狭缝进入右侧磁场，分别做匀速圆周运动，求出半径，画出恰好分离时的轨迹图即PF的最大值。

(1)因正离子在AB极与CD极间加速，则知AB极电势高，

离子在AB与CD两极间加速，由动能定理有qU＝mv2，

得离子到达CD极时的速度v＝.

(2)正离子在Ⅰ区做匀加速直线运动，设所用时间为t1，则t1＝＝

设离子在Ⅱ区做匀速直线运动的时间为t2，则t2＝＝2，

离子在Ⅲ区先匀减速，后反向匀加速，设加速度为a，所用时间为t3，

有a＝＝，t3＝2·，解得t3＝4，

则总时间t＝t1＋t2＋t3，代入得k＝

(3)设质量为M和m的离子在磁场中做圆周运动的半径为R1和R2，洛伦兹力提供向心力，

由qvB＝，可得R1＝，R2＝

得半径关系，因为1<≤4，故1<≤2，

作出两种离子在磁场中运动的临界情况(即质量为M的正离子在收集板上的最低点与质量为m的正离子在收集板上的最高点重合)如图所示，

此时狭缝最大值x应满足x＝2R1－2R2，d＝2R1＋x，解得x＝d．