题目内容
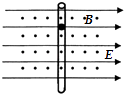
【题目】距地面高5m的水平直轨道上A、B两点相距2m,在B点用细线悬挂一小球,离地高度为h,如图.小车始终以4m/s的速度沿轨道匀速运动,经过A点时将随车携带的小球由轨道高度自由卸下,小车运动至B点时细线被轧断,最后两球同时落地.不计空气阻力,取重力加速度的大小g=10m/s2 . 可求得h等于( )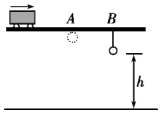
A.1.25 m
B.2.25 m
C.3.75 m
D.4.75 m
【答案】A
【解析】解:设轨道离地的高度为H,则知 H=5m
经过A点,将球自由卸下后,A球做平抛运动,则有:
H= ![]() gt12
gt12
解得:t1=1s
小车从A点运动到B点的时间 t2= ![]() =
= ![]() s=0.5s
s=0.5s
因为两球同时落地,则细线被轧断后B处小球做自由落体运动的时间为 t3=t1﹣t2=1﹣0.5=0.5s
则 h= ![]() gt22=
gt22= ![]() ×10×0.52=1.25m
×10×0.52=1.25m
故答案为:A
分析两个小球的运动A球做平抛运动,B处小球做自由落体运动,两球同时落地根据自由落体运动规律,平抛运动公式可以求解。

练习册系列答案
相关题目