题目内容

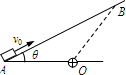
如图所示，倾斜角度为θ的粗糙程度均匀的绝缘斜面，下方O点处有一带电量为+Q的点电荷，质量为m、带电量为-q的小物体（可看成质点）与斜面间的动摩擦因数为μ．现使小物体以初速度v0从斜面上的A点沿斜面上滑，到达B点时速度为零，然后又下滑回到A点．小物体所带电荷量保持不变，静电力常数为k，重力加速度为g，OA=OB=l．求：
（1）小物体沿斜面上滑经过AB中点时的加速度；
（2）小物体返回到斜面上的A点时的速度．
（1）小物体经过AB中点时，根据牛顿第二定律和库仑定律得：
FN=mgcosθ+k
Qq
(lsinθ)2

mgsinθ+μFN=ma
得：a=gsinθ+μ（gcosθ+
kQq
m(lsinθ)2
）
（2）设物体上升过程中，摩擦力做功为Wf．由于OA=OB，A、B两点的电势相等，上升和下滑过程中电场力做功都为0，则根据动能定理得
上升过程，有 0-
1
2
mv02=-mglsin2θ+Wf
下滑过程，有
1
2
mv2=mglsin2θ+Wf
解得：v=
4glsin2θ-
v20

答：
（1）小物体沿斜面上滑经过AB中点时的加速度是gsinθ+μ（gcosθ+
kQq
m(lsinθ)2
）；
（2）小物体返回到斜面上的A点时的速度是
4glsin2θ-
v20
．
练习册系列答案
相关题目
如图所示，把小车放在倾角为30°的光滑斜面上，用轻绳跨过定滑轮使之与盛有沙子的小桶相连，不计滑轮质量及摩擦，已知小车的质量为3m，小桶与沙子的总质量为m，小车从静止释放后，在小桶上升竖直高度为h的过程中（　　）
A．小桶处于失重状态B．小桶的最大速度为
1
2
gh
C．小车受绳的拉力等于mgD．小车的最大动能为mgh
起重机将质量为500kg的物体由静止竖直向上吊起2m高，此时物体的速度大小为1m/s，如果g取10m/s2，则（　　）
A．起重机对物体做功250J
B．起重机对物体做功1.025×104J
C．物体受到的合力对它做功250J
D．物体受到的合力对它做功1.025×104J
如图所示，AB和CDO都是处于竖直平面内的光滑圆弧形轨道，OA处于水平位置．AB是半径为R=2m的
1
4
圆周轨道，CDO是半径为r=1m的半圆轨道，最高点O处固定一个竖直弹性档板．D为CDO轨道的中央点．BC段是水平粗糙轨道，与圆弧形轨道平滑连接．已知BC段水平轨道长L=2m，与小球之间的动摩擦因数μ=0.4．现让一个质量为m=1kg的小球P从A点的正上方距水平线OA高H处自由落下．（取g=10m/s2）
（1）当H=1.4m时，问此球第一次到达D点对轨道的压力大小．
（2）当H=1.4m时，试通过计算判断此球是否会脱离CDO轨道．如果会脱离轨道，求脱离前球在水平轨道经过的路程．如果不会脱离轨道，求静止前球在水平轨道经过的路程．
如图所示为固定在竖直平面内的光滑轨道ABCD，其中ABC部分为半径R=0.9m的半圆形轨道，CD部分为水平轨道．一个质量m=1kg的小球沿水平方向进入轨道，通过最高点A时对轨道的压力为其重力的3倍．小球运动过程中所受空气阻力忽略不计，g取10m/s2．
（1）画出小球在A点时的受力示意图：
（2）求出小球在A点时的速度大小vA；
（3）求出小球经过C点进入半圆形轨道时对轨道的压力NC．
如图所示，一位质量m=60kg，参加“挑战极限运动”的业余选手，要越过一宽为s=2.5m的水沟后跃上高为h=2.0m的平台．他采用的方法是：手握一根长L=3.25m的轻质弹性杆一端，从A点由静止开始加速助跑，至B点时杆另一端抵在O点的阻挡物上，接着杆发生形变，同时人蹬地后被弹起，到达最高点时杆处于竖直状态，人的重心在杆的顶端，此刻人放开杆水平飞出并趴落到平台上，运动过程中空气阻力可忽略不计．（g取10m/s2）求：
（1）人要最终到达平台，在最高点飞出时刻的速度应至少多大？
（2）设人到达B点时速度υB=8m/s，人受的阻力为体重的0.1倍，助跑距离sAB=16m，则人在该过程中做的功为多少？
（3）设人跑动过程中重心离地高度H=0.8m，在（1）、（2）两问的条件下，人要越过一宽为s=2.5m的水沟后跃上高为h=2.0m的平台，在整个过程中人应至少要做多少功？
两个物体的质量分别为m1和m2，且m1=4m2，当它们以相同的动能在动摩擦因数相同的水平面上滑行时，它们滑行的距离之比s1：s2和滑行的时间之比t1：t2分别：（　　）
A．1：4，1：2B．4：1、2：1C．1：4、2：1D．4：1、4：1
如图所示，质量为m、电荷量为+q的滑块，静止在绝缘水平面上．某时刻，在MN的左侧加一个场强为E的匀强电场，滑块在电场力的作用下开始向右运动．已知滑块与MN之间的距离为d，滑块与水平面间的动摩擦因数为μ，重力加速度为g．求：
（1）滑块在电场中运动时加速度a的大小；
（2）滑块停止时与MN间的距离x．
如图所示为半径R=0.50m的四分之一圆弧轨道，底端距水平地面的高度h=0.45m．一质量m=1.0kg的小滑块从圆弧轨道顶端A由静止释放，到达轨道底端B点的速度v=2.0m/s．忽略空气的阻力．取g=10m/s2．求：
（1）小滑块在圆弧轨道底端B点受到的支持力大小FN；
（2）小滑块由A到B的过程中，克服摩擦力所做的功W；
（3）小滑块落地点与B点的水平距离x．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网