题目内容
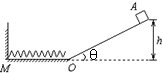
如图所示为半径R=0.50m的四分之一圆弧轨道,底端距水平地面的高度h=0.45m.一质量m=1.0kg的小滑块从圆弧轨道顶端A由静止释放,到达轨道底端B点的速度v=2.0m/s.忽略空气的阻力.取g=10m/s2.求:
(1)小滑块在圆弧轨道底端B点受到的支持力大小FN;
(2)小滑块由A到B的过程中,克服摩擦力所做的功W;
(3)小滑块落地点与B点的水平距离x.
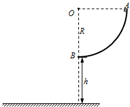
(1)小滑块在圆弧轨道底端B点受到的支持力大小FN;
(2)小滑块由A到B的过程中,克服摩擦力所做的功W;
(3)小滑块落地点与B点的水平距离x.

(1)小滑块在圆弧轨道底端B点受重力和支持力,
根据牛顿第二定律,FN-mg=m
解得:FN=18N
(2)小滑块由A到B的过程中,根据动能定理得,
mgR-W=
mv2 ,
解得:W=mgR-
mv2 =3J
(3)小滑块从B点出发做平抛运动,根据平抛运动的规律得
水平方向:x=vt
竖直方向:h=
gt2
解得:x=0.6m
答:(1)小滑块在圆弧轨道底端B点受到的支持力大小是18N;
(2)小滑块由A到B的过程中,克服摩擦力所做的功是3J;
(3)小滑块落地点与B点的水平距离是0.6m.
根据牛顿第二定律,FN-mg=m
| v2 |
| R |
解得:FN=18N
(2)小滑块由A到B的过程中,根据动能定理得,
mgR-W=
| 1 |
| 2 |
解得:W=mgR-
| 1 |
| 2 |
(3)小滑块从B点出发做平抛运动,根据平抛运动的规律得
水平方向:x=vt
竖直方向:h=
| 1 |
| 2 |
解得:x=0.6m
答:(1)小滑块在圆弧轨道底端B点受到的支持力大小是18N;
(2)小滑块由A到B的过程中,克服摩擦力所做的功是3J;
(3)小滑块落地点与B点的水平距离是0.6m.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目