题目内容
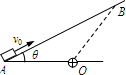
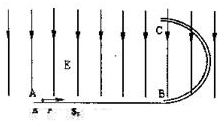
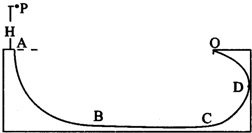
如图所示,AB和CDO都是处于竖直平面内的光滑圆弧形轨道,OA处于水平位置.AB是半径为R=2m的
圆周轨道,CDO是半径为r=1m的半圆轨道,最高点O处固定一个竖直弹性档板.D为CDO轨道的中央点.BC段是水平粗糙轨道,与圆弧形轨道平滑连接.已知BC段水平轨道长L=2m,与小球之间的动摩擦因数μ=0.4.现让一个质量为m=1kg的小球P从A点的正上方距水平线OA高H处自由落下.(取g=10m/s2)
(1)当H=1.4m时,问此球第一次到达D点对轨道的压力大小.
(2)当H=1.4m时,试通过计算判断此球是否会脱离CDO轨道.如果会脱离轨道,求脱离前球在水平轨道经过的路程.如果不会脱离轨道,求静止前球在水平轨道经过的路程.
| 1 |
| 4 |
(1)当H=1.4m时,问此球第一次到达D点对轨道的压力大小.
(2)当H=1.4m时,试通过计算判断此球是否会脱离CDO轨道.如果会脱离轨道,求脱离前球在水平轨道经过的路程.如果不会脱离轨道,求静止前球在水平轨道经过的路程.

(1)设小球第一次到达D的速度VD,P到D点的过程对小球根据动能定理列式,有:
mg(H+r)-μmgL=
mVD2
在D点对小球列牛顿第二定律:FN=m
联立解得:FN=32N
(2)第一次来到O点,速度V1
P到O点的过程对小球根据动能定理列式,有:
mgH-μmgL=
mV12
解得:V12=12
要能通过O点,须mg<m
临界速度VO2=10
故第一次来到O点之前没有脱离,第二次来到D点是沿着原路返回,设第三次来到D点的动能EK
对之前的过程根据动能定理列式,有:
mg(H+r)-3μmgL=EK
代入解得:EK=0
故小球一直没有脱离CDO轨道
设此球静止前在水平轨道经过的路程S
对全过程根据动能定理列式,有:
mg(H+R)-μmgS=0
解得:S=8.5m
答:(1)当H=1.4m时,此球第一次到达D点对轨道的压力大小为32N.(2)当H=1.4m时,此球不会脱离CDO轨道,静止前球在水平轨道经过的路程为8.5m.
mg(H+r)-μmgL=
| 1 |
| 2 |
在D点对小球列牛顿第二定律:FN=m
| ||
| r |
联立解得:FN=32N
(2)第一次来到O点,速度V1
P到O点的过程对小球根据动能定理列式,有:
mgH-μmgL=
| 1 |
| 2 |
解得:V12=12
要能通过O点,须mg<m
| v2 |
| r |
临界速度VO2=10
故第一次来到O点之前没有脱离,第二次来到D点是沿着原路返回,设第三次来到D点的动能EK
对之前的过程根据动能定理列式,有:
mg(H+r)-3μmgL=EK
代入解得:EK=0
故小球一直没有脱离CDO轨道
设此球静止前在水平轨道经过的路程S
对全过程根据动能定理列式,有:
mg(H+R)-μmgS=0
解得:S=8.5m
答:(1)当H=1.4m时,此球第一次到达D点对轨道的压力大小为32N.(2)当H=1.4m时,此球不会脱离CDO轨道,静止前球在水平轨道经过的路程为8.5m.

练习册系列答案
相关题目