题目内容

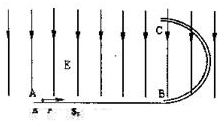
如图所示，质量为m、电荷量为+q的滑块，静止在绝缘水平面上．某时刻，在MN的左侧加一个场强为E的匀强电场，滑块在电场力的作用下开始向右运动．已知滑块与MN之间的距离为d，滑块与水平面间的动摩擦因数为μ，重力加速度为g．求：
（1）滑块在电场中运动时加速度a的大小；
（2）滑块停止时与MN间的距离x．
（1）根据牛顿第二定律有：
qE-f=ma

mg-N=0

又因为：f=μN
所以有：a=
qE-μmg
m

（2）小物块在整个运动过程中，根据动能定理有：
（qE-μmg）d-μmgx=0-0
所以：x=
(qE-μmg)d
μmg

答：（1）滑块在电场中运动时加速度a的大小为
qE-μmg
m
；
（2）滑块停止时与MN间的距离x=
(qE-μmg)d
μmg
练习册系列答案
相关题目
如图所示，斜面足够长，其倾角为α，质量为m的滑块，距挡板P为s0，以初速度v0沿斜面上滑，滑块与斜面间的动摩擦因数为μ，滑块所受摩擦力小于滑块沿斜面方向的重力分力，若滑块每次与挡板相碰均无机械能损失（即速度大小不变方向相反），求滑块在斜面上经过的总路程为多少？
如图所示，倾斜角度为θ的粗糙程度均匀的绝缘斜面，下方O点处有一带电量为+Q的点电荷，质量为m、带电量为-q的小物体（可看成质点）与斜面间的动摩擦因数为μ．现使小物体以初速度v0从斜面上的A点沿斜面上滑，到达B点时速度为零，然后又下滑回到A点．小物体所带电荷量保持不变，静电力常数为k，重力加速度为g，OA=OB=l．求：
（1）小物体沿斜面上滑经过AB中点时的加速度；
（2）小物体返回到斜面上的A点时的速度．
据报道，嫦娥三号将于近期发射．嫦娥三号接近月球表面的过程可简化为三个阶段：距离月球表面15km时打开反推发动机减速，下降到距月球表面H=l00m高度时悬停，寻找合适落月点；找到落月点后继续下降，距月球表面h=4m时速度再次减为0；此后，关闭所有发动机，使它做自由落体运动落到月球表面．已知嫦娥三号质量为
140kg，月球表面重力加速度g'约为1.6m/s2，月球半径为R，引力常量G．求：
（l）月球的质量；
（2）嫦娥三号悬停在离月球表面l00m处时发动机对嫦娥三号的作用力；
（3）嫦娥三号从悬停在l00m处到落至月球表面，发动机对嫦娥三号做的功．
如图1所示，AB段是一段光滑的水平轨道，轻质弹簧一端固定在A点，放置在轨道AB上，BC段是半径R=2.5m的光滑半圆弧轨道，有一个质量m=0.1kg的小滑块，紧靠在被压紧的弹簧前，松开弹簧，物块被弹出后恰好能通过C点，（g取10m/s2）

求：（1）弹簧被压紧时的弹性势能；
（2）保持弹簧每次的压缩量相同，让物块的质量在
1
4
m至m之间变化，求物块从C点飞出后在水平轨道上落点的范围；
（3）保持物块的质量m不变，改变每次对弹簧的压缩量，设小滑块经过半圆弧轨道C点时，轨道对小滑块作用力的大小为FN，试研究FN与弹簧的弹性势能EP的函数关系，并在坐标纸上作出FN-EP图象．
如图，在水平向左的匀强电场和垂纸面向里的匀强磁场中，E=4V/m，B=2T，一质量为m=1.0×l0-3kg的带正电的小物块P带电量q=2.5×10-3C，从绝缘粗糙的竖直墙壁的A点无初速下滑，物体与墙壁间动摩擦因数μ=0.5，当它向下滑行h=0.8m到达C点时，离开墙壁做曲线运动，当它运动到与墙的水平距离为0.6m时，竖直方向下落的高度即D与A的高度差H=1.6m．（g=l0m/s2）
A．物块下滑过程中克服摩擦力做功为4×10-3J
B．物块下滑过程中克服摩擦力做功为6×10-3J
C．物块下滑到C点时速度大小为2m/s
D．物块下滑到D点时速度大小为2
3
m/s
某学校科技小组对一辆自制小遥控车的性能进行研究，他们让小车在水平地面上由静止开始运动，并将小车运动的全过程记录下来，通过数据处理得到如图所示的v-t图象，已知小车在0-2s内做匀加速直线运动，2-10s内小车牵引力的功率保持不变，在10s末停止遥控，关闭电动机．小车的质量m=1kg，整个过程中小车受到的阻力保持不变．求：
（1）小车所受的阻力f；
（2）小车在2-10s内牵引力的功率；
（3）小车在14s内阻力f做的功．
有一玩具汽车绝缘上表面固定一个带负电物块，它们的总质量m=0.5kg，物块带电量q=-5.0×10-5c．现把玩具汽车放置在如图所示的水平直轨道A点，BC由光滑管道弯曲而成的半圆轨道，玩具汽车在光滑管道中能自由运动，整个轨道所处空间存在竖直向下的匀强电场，其电场强度大小E=6.0×l04N/c．玩具汽车在水平直轨道运动时阻力恒为Ff=0.5N，通电后玩具汽车以恒定功率P=l0w行驶，通电1.0s自动断电，断电后玩具汽车能以一定的速度从B点进入半圆轨道．已知AB间距L=4.0m，g取l0m/s2（玩具汽车可看成质点，整个运动过程物块带电量不变）．
①若半圆轨道半径R=0.4m，玩具汽车进入管道中B点时对管道的压力多大？
②当半圆轨道半径R满足什么条件时，玩具汽车能再次回到A点？
如图所示，斜面倾角为37°，斜面长为5m，一物体从斜面顶端静止滑下，物体与平面、斜面间的动摩擦因数均为0.3．求该物体下滑后将在距斜面底端多远处停止？（g=10m/s2）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网