题目内容
(16分)小车上有一个固定支架,支架上用长为 的绝缘细线悬挂质量为m、电量为q的小球,处于水平方向的匀强电场中。小车在距离矮墙x处,向着矮墙从静止开始做加速度a匀加速运动,此时,细线刚好竖直,如图所示。当小车碰到矮墙时,立即停止运动,且电场立刻消失。已知细线最大承受拉力为7mg。
的绝缘细线悬挂质量为m、电量为q的小球,处于水平方向的匀强电场中。小车在距离矮墙x处,向着矮墙从静止开始做加速度a匀加速运动,此时,细线刚好竖直,如图所示。当小车碰到矮墙时,立即停止运动,且电场立刻消失。已知细线最大承受拉力为7mg。
⑴求匀强电场的电场强度;
⑵若小球能通过最高点,写出最高点时细线的拉力与x的关系式;
⑶若要使细线不断裂也不松弛,确定x的取值范围。
⑴E= ;⑵T=
;⑵T= -5mg;⑶x≤
-5mg;⑶x≤ 或
或 ≤x≤
≤x≤
解析试题分析:⑴对小球受重力mg、细线的拉力T和电场力qE作用,根据牛顿第二定律可知qE=ma
解得匀强电场的电场强度为:E=
⑵根据匀变速直线运动规律可知,当小车碰到矮墙瞬间小球的速度为:v1=
小车停止运动后,小球受mg、细线的拉力T作用,在竖直平面内做圆周运动,此时只有重力mg做功,根据动能定理有:-2mgL= -
-
在小球运动至圆轨迹最高点时,根据牛顿第二定律和向心力公式有:T+mg=
联立以上各式解得:T= -5mg
-5mg
⑶若小球仅在下半圆周内摆动,则:mgL≥
解得:x≤
此情况中,在最低点有:T-mg=
解得:T=3mg<7mg,符合题意要求
若小球完成完整的圆周运动,则:T2= -5mg≥0
-5mg≥0
且:T1= +mg≤7mg
+mg≤7mg
联立以上各式解得: ≤x≤
≤x≤
所以要使细线不断裂也不松弛, x的取值范围为:x≤ 或
或 ≤x≤
≤x≤
考点:本题主要考查了匀变速直线运动规律、圆周运动向心力公式、牛顿第二定律、动能定理的应用以及临界情况的分析能力问题,属于中档偏高题。

练习册系列答案
相关题目
 。
。 =8s时到达高度h
=8s时到达高度h =6s时遥控器出现故障,飞行器立即失去牵引力。求此次飞行器能达到的最大高度h
=6s时遥控器出现故障,飞行器立即失去牵引力。求此次飞行器能达到的最大高度h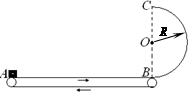

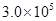 km的月球,也发射了一种类似四轮小车的月球探测器.它能够在自动导航系统的控制下行走,且每隔10s向地球发射一次信号.探测器上还装着两个相同的减速器(其中一个是备用的),这种减速器可提供的最大加速度为5
km的月球,也发射了一种类似四轮小车的月球探测器.它能够在自动导航系统的控制下行走,且每隔10s向地球发射一次信号.探测器上还装着两个相同的减速器(其中一个是备用的),这种减速器可提供的最大加速度为5 .某次探测器的自动导航系统出现故障,从而使探测器只能匀速前进而不再能自动避开障碍物.此时地球上的科学家必须对探测器进行人工遥控操作.下表为控制中心的显示屏的数据:(信号传送速度等于光速:C=
.某次探测器的自动导航系统出现故障,从而使探测器只能匀速前进而不再能自动避开障碍物.此时地球上的科学家必须对探测器进行人工遥控操作.下表为控制中心的显示屏的数据:(信号传送速度等于光速:C=


 做匀减速运动,恰到该小站停止,停车lmin后再以
做匀减速运动,恰到该小站停止,停车lmin后再以 的加速度匀加速直线启动,直到恢复原速行驶。求该列车由于临时停车,共耽误多长时间。
的加速度匀加速直线启动,直到恢复原速行驶。求该列车由于临时停车,共耽误多长时间。