题目内容
（10分）在消防演习中，消防队员从一根竖直的长直轻绳上由静止滑下，经一段时间落地．为了获得演习中的一些数据，以提高训练质量，研究人员在轻绳上端安装一个力传感器并与数据处理系统相连接，用来记录消防队员下滑过程中轻绳受到的拉力与消防队员重力的比值随时间变化的情况．已知某队员在一次演习中的收集的数据如图所示，
(1)求该消防队员在下滑过程中的最大速度和落地速度各是多少？（g取10m/s2)
(2)消防队员在下滑过程总位移？
(1)4m/s,1m/s (2)5.75m
解析试题分析：（1）该队员先在t1=1s时间内以a1匀加速下滑．
然后在t2=1.5s时间内以a2匀减速下滑．
第1s由牛顿第二定律得：mg－F1=ma1
所以a1=
=4m/s2
最大速度vm=a1t1
代入数据解得：vm="4m/s"
后1.5s由牛顿第二定律得：F2－mg=ma2
a2=
=2m/s2
队员落地时的速度v=vm－a2t2
代入数据解得：v="1m/s"
(2) 防队员在下滑过程总位移:
考点：本题考查了匀变速直线运动的规律
练习册系列答案
相关题目
汽车起动的快慢和能够达到的最大速度，是衡量汽车性能的指标体系中的两个重要指标。汽车起动的快慢用车的速度从0到100km/h的加速时间来表示，这个时间越短，汽车起动的加速度就越大。下表中列出了两种汽车的性能指标(为了简化计算，把100km/h取为30m/s)。
| | 起动的快慢（单位：s） (0～30m/s的加速时间) | 最大速度（m/s） |
| 甲车 | 12 | 40 |
| 乙车 | 6 | 50 |
(1)甲、乙两车的起动加速度分别是多少?
(2)相遇时乙车发生的位移是多少?
(3)甲车比乙车提前运动的时间为多少?
.求：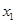
；
.
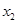的绝缘细线悬挂质量为m、电量为q的小球，处于水平方向的匀强电场中。小车在距离矮墙x处，向着矮墙从静止开始做加速度a匀加速运动，此时，细线刚好竖直，如图所示。当小车碰到矮墙时，立即停止运动，且电场立刻消失。已知细线最大承受拉力为7mg。
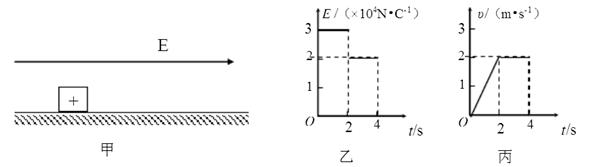
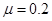。从t=0开始，物体受到一个大小和方向呈周期性变化的水平力F的作用，力F 随时间的变化规律如图9所示。重力加速度
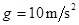， 求：
的大小和方向；
时物块运动的瞬时速度
的大小和方向；