��Ŀ����
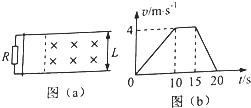
����Ŀ����ͼ����ʾ���ռ����һ�н���ǿ�ų����ų�����߽���������ʾ�������Ҳ��㹻��������ڴų����ų�������ֱ���£��ڹ⻬��Եˮƽ������һ�����ν����߿�ab�߳�Ϊl=0.2m���߿�����m=0.1kg������R=0.1������ˮƽ���ҵ�����F�����£��Գ��ٶ�v0=1m/s�ȼ��ٽ���ų�������F��С��ʱ��t�仯��ͼ����ͼ����ʾ�����߿��ұ߸ս���ų�ʱ��ʼ��ʱ���� 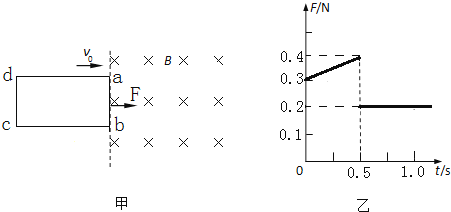
��1����ǿ�ų��ĴŸ�Ӧǿ��B
��2���߿����ų��Ĺ����У�ͨ���߿�ĵ����q��
��3�����߿����ų�������F����ΪWF=0.27J�����ڴ˹������߿�����Ľ�����Q ��
���𰸡�
��1��
��F��tͼ���֪�����߿�ȫ������ų���
F=0.2Nʱ���߿�ļ��ٶȣ� ![]() ��
��
0ʱ���߿����ܵİ������� ![]() ��
��
��ͼʾͼ���֪��F=0.3N��
��ţ�ٵڶ����ɵã�F��F��=ma��
�������ݽ�ã�B=0.5T��
��2��
�߿����ų�����ͨ�����������q=I��t��
�ɷ����ڵ�Ÿ�Ӧ���ɵ� ![]() ��
��
�ɱպϵ�·ŷķ���ɵã� ![]() ��
��
��������� ![]() ��
��
���ȱ���ֱ���˶��ã� ![]() ��
��
�������ݽ�ã�x=0.75m��q=0.75C��
��3��
�߿����ų����̣��������غ㶨�ɣ�
![]() ���������ݽ�ã�Q=0.12J
���������ݽ�ã�Q=0.12J
����������1����F��tͼ���֪�����߿�ȫ������ų���
F=0.2Nʱ���߿�ļ��ٶȣ� ![]() ��
��
0ʱ���߿����ܵİ������� ![]() ��
��
��ͼʾͼ���֪��F=0.3N��
��ţ�ٵڶ����ɵã�F��F��=ma ��
�������ݽ�ã�B=0.5T����2���߿����ų�����ͨ�����������q=I��t ��
�ɷ����ڵ�Ÿ�Ӧ���ɵ� ![]() ��
��
�ɱպϵ�·ŷķ���ɵã� ![]() ��
��
��������� ![]() ��
��
���ȱ���ֱ���˶��ã� ![]() ��
��
�������ݽ�ã�x=0.75m��q=0.75C����3���߿����ų����̣��������غ㶨�ɣ�![]() ���������ݽ�ã�Q=0.12J��
���������ݽ�ã�Q=0.12J��
�����㾫����������Ĺؼ�����������ζ��ɵ����֪ʶ��������ζ���������һ������ĸ�Ӧ����������ж��������ֶ���ֻ�����ڵ����и�Ÿ����˶��������������������ֶ����ж�������ζ����ж���㣮

 ȫ��������ϵ�д�
ȫ��������ϵ�д� һ��һ����ʱ���ϵ�д�
һ��һ����ʱ���ϵ�д�