题目内容
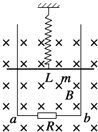
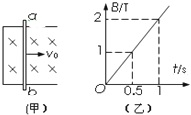
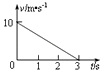
【题目】如图（a），两相距L=0.5m的平行金属导轨固定于水平面上，导轨左端与阻值R=2Ω的电阻连接，导轨间虚线右侧存在垂直导轨平面的匀强磁场．质量m=0.2kg的金属杆垂直置于导轨上，与导轨接触良好，导轨与金属杆的电阻可忽略．杆在水平向右的恒定拉力作用下由静止开始运动，并始终与导轨垂直，其v﹣t图象如图（b）所示．在15s时撤去拉力，同时使磁场随时间变化，从而保持杆中电流为0．求：
（1）金属杆所受拉力的大小F；
（2）0﹣15s内匀强磁场的磁感应强度大小B0；
（3）15﹣20s内磁感应强度随时间变化规律．
【答案】
（1）
由v﹣t图象可知，在0﹣10内，金属杆做匀加速直线运动，杆没有进入磁场，
由牛顿第二定律得：F﹣μmg=ma1，
由题意可知，15s末撤去拉力，没有感应电流，杆不受安培力作用，
杆所受的合外力为滑动摩擦力，由牛顿第二定律得：μmg=ma2，
由v﹣t图象可知，加速度： 
， 
，
解得：F=0.24N；
（2）
在10﹣15s内，金属杆做匀速直线运动，速度：v=4m/s，
金属杆受到的安培力： 
，
金属杆做匀速直线运动，处于平衡状态，
由平衡条件得： 
，代入数据解得：B0=0.4T；
（3）
15﹣20s内部产生感应电流，穿过回路的磁通量保持不变，
金属杆在10﹣15s内的位移：d=vt=4×5=20m，
在15s后的金属杆的加速度：a=a2=0.8m/s2，
金属杆的位移： 
，
磁通量保持不变，则：B0Ld=BL（d+x），
解得： 
；
【解析】（1）由v﹣t图象可知，在0﹣10内，金属杆做匀加速直线运动，杆没有进入磁场，
由牛顿第二定律得：F﹣μmg=ma1 ，
由题意可知，15s末撤去拉力，没有感应电流，杆不受安培力作用，
杆所受的合外力为滑动摩擦力，由牛顿第二定律得：μmg=ma2 ，
由v﹣t图象可知，加速度： ， ，
解得：F=0.24N；（2）在10﹣15s内，金属杆做匀速直线运动，速度：v=4m/s，
金属杆受到的安培力： ，
金属杆做匀速直线运动，处于平衡状态，
由平衡条件得： ，代入数据解得：B0=0.4T；（3）15﹣20s内部产生感应电流，穿过回路的磁通量保持不变，
金属杆在10﹣15s内的位移：d=vt=4×5=20m，
在15s后的金属杆的加速度：a=a2=0.8m/s2 ，
金属杆的位移： ，
磁通量保持不变，则：B0Ld=BL（d+x） ，
解得： ；
（1）根据金属杆的受力情况，由牛顿第二定律列方程，由v﹣t求出求出金属杆的加速度，然后求出拉力F ． （2）应用安培力公式求出安培力，然后应用平衡条件求出磁感应强度．（3）当穿过回路的磁通量不变时不产生感应电流，据此求出磁感应强度的变化规律．
