题目内容
(10分)如图所示的水平转盘可绕竖直轴OO′旋转,盘上水平杆上穿着两个质量均为m=2kg的小球A和B。现将A和B分别置于距轴rA=0.5m和rB=1m处,并用不可伸长的轻绳相连。已知两球与杆之间的最大静摩擦力都是fm=1N。试分析转速ω从零缓慢逐渐增大(短时间内可近似认为是匀速转动),两球对轴保持相对静止过程中,在满足下列条件下,ω的大小。
(1)绳中刚要出现张力时的ω1;
(2)A、B中某个球所受的摩擦力刚要改变方向时的ω2,并指明是哪个球的摩擦力方向改变;
(3)两球对轴刚要滑动时的ω3。
见试题分析
解析试题分析:(1)当ω较小时, fA=FAn=mω2rA,fB=FBn=mω2rB,
因rB>rA,所以B将先滑动。
对B球:fm=FBn=mω12rB,
解得: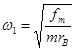 =
=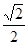 (rad/s)≈0.7(rad/s)。
(rad/s)≈0.7(rad/s)。
(2)当绳上出现张力以后,对B球:fm+T=FBn=mω2rB,对A球:fA+T=FAn=mω2rA,
当ω增大时,T增大,fA减小,当fA减小到0时,
对A球:T=FAn=mω22rA, 对B球:fm+T=FBn=mω22rB,
联立解得: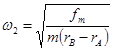 =" 1" (rad/s)。
=" 1" (rad/s)。
(3)当ω再增大时,fA将改向向外,直至随B球一起向B球一侧滑动。
刚要滑动时: 对A球:T- fm =FAn=mω32rA, 对B球:fm+T=FBn=mω32rB,
联立解得: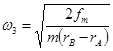 =
= 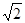 (rad/s) ≈1.4(rad/s)。
(rad/s) ≈1.4(rad/s)。
考点:圆周运动 牛顿第二定律

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,不计一切摩擦和阻力。求:
,不计一切摩擦和阻力。求:

 ,电场宽度均为d,水平面粗糙摩擦系数为μ,一个质量为m,带正电的、电荷量为q的物体(看作质点),从第一个向右的电场区域的边缘由静止进入电场,则物体从开始运动到离开第2n个电场区域的过程中,求:
,电场宽度均为d,水平面粗糙摩擦系数为μ,一个质量为m,带正电的、电荷量为q的物体(看作质点),从第一个向右的电场区域的边缘由静止进入电场,则物体从开始运动到离开第2n个电场区域的过程中,求:


 的电阻,导轨电阻不计,磁感应强度B=0.5T的匀强磁场垂直导轨平面向上。一根质量为m=0.2kg、电阻r=4
的电阻,导轨电阻不计,磁感应强度B=0.5T的匀强磁场垂直导轨平面向上。一根质量为m=0.2kg、电阻r=4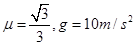 。求
。求