题目内容
(20分)如图所示,平行金属导轨PQ、MN相距d=2m,导轨平面与水平面夹角a= 30°,导轨上端接一个R=6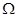 的电阻,导轨电阻不计,磁感应强度B=0.5T的匀强磁场垂直导轨平面向上。一根质量为m=0.2kg、电阻r=4
的电阻,导轨电阻不计,磁感应强度B=0.5T的匀强磁场垂直导轨平面向上。一根质量为m=0.2kg、电阻r=4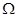 的金属棒ef垂直导轨PQ、MN静止放置,距离导轨底端xl=3.2m。另一根绝缘塑料棒gh与金属棒ef平行放置,绝缘塑料棒gh从导轨底端以初速度v0=l0m/s沿导轨上滑并与金属棒正碰(碰撞时间极短),磁后绝缘塑料棒gh沿导轨下滑,金属棒ef沿导轨上滑x2=0.5m后停下,在此过程中电阻R上产生的电热为Q=0.36J。已知两棒与导轨间的动摩擦因数均为
的金属棒ef垂直导轨PQ、MN静止放置,距离导轨底端xl=3.2m。另一根绝缘塑料棒gh与金属棒ef平行放置,绝缘塑料棒gh从导轨底端以初速度v0=l0m/s沿导轨上滑并与金属棒正碰(碰撞时间极短),磁后绝缘塑料棒gh沿导轨下滑,金属棒ef沿导轨上滑x2=0.5m后停下,在此过程中电阻R上产生的电热为Q=0.36J。已知两棒与导轨间的动摩擦因数均为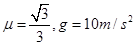 。求
。求
(1)绝缘塑料棒gh与金属棒ef碰撞前瞬间,绝缘塑料棒的速率;
(2)碰撞后金属棒ef向上运动过程中的最大加速度;
(3)金属棒ef向上运动过程中通过电阻R的电荷量。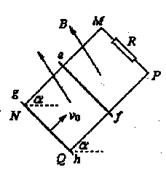
(1)6m/s (2) 12 m/s2 (3)0.05C
解析试题分析:(1)绝缘塑料棒与金属棒相碰前,做匀减速直线运动
由牛顿第二定律得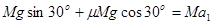
由运动学公式得: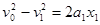
解得v1=6m/s
(2)设金属棒刚开始运动时速度为v,由能量守恒定律得: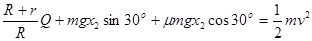
解得:v=4 m/s
金属棒刚开始运动时加速度最大,此时感应电动势E="Bdv=4V" 感应电流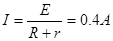
安培力F=BId=0.4N
由牛顿第二定律得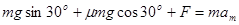
解得am="12" m/s2
(3)通过电阻R的电荷量为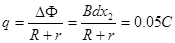
考点:本题考查电磁感应定律、动能定理、牛顿第二定律

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

 内存在水平向右的匀强电场,场强大小E=10N/c,在y≥0的区域内还存在垂直于坐标平面向里的匀强磁场,磁感应强度大小B=0.5T一带电量
内存在水平向右的匀强电场,场强大小E=10N/c,在y≥0的区域内还存在垂直于坐标平面向里的匀强磁场,磁感应强度大小B=0.5T一带电量 、质量
、质量 的小球由长
的小球由长 的细线悬挂于
的细线悬挂于 点小球可视为质点,现将小球拉至水平位置A无初速释放,小球运动到悬点
点小球可视为质点,现将小球拉至水平位置A无初速释放,小球运动到悬点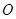 时,悬线突然断裂,此后小球又恰好能通过
时,悬线突然断裂,此后小球又恰好能通过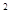 ),求:
),求: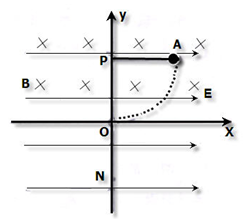
 间的距离。
间的距离。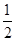 B0后保持不变,同时将导体棒解除锁定,导体棒向下运动,离开导轨时的速度为v.导体棒与导轨始终保持良好接触,导轨电阻不计,重力加速度为g.求导体棒:
B0后保持不变,同时将导体棒解除锁定,导体棒向下运动,离开导轨时的速度为v.导体棒与导轨始终保持良好接触,导轨电阻不计,重力加速度为g.求导体棒: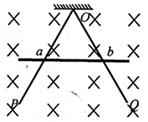
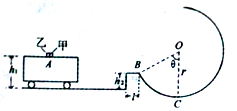
 =1.4。求:
=1.4。求:
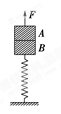
 导轨上停放一质量为m="0.10" kg、电阻r="0.20"
导轨上停放一质量为m="0.10" kg、电阻r="0.20" 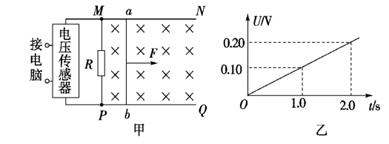
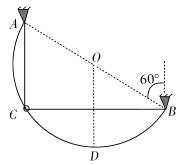
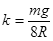 的弹性轻绳穿过圆环且固定在A、B两点。已知弹性轻绳满足胡克定律,且形变量为x时具有弹性势能
的弹性轻绳穿过圆环且固定在A、B两点。已知弹性轻绳满足胡克定律,且形变量为x时具有弹性势能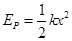 ,重力加速度为g,不计一切摩擦。将圆环由A点正下方的C点静止释放,当圆环运动到导轨的最低点D点时,求
,重力加速度为g,不计一切摩擦。将圆环由A点正下方的C点静止释放,当圆环运动到导轨的最低点D点时,求