题目内容
如图所示,在粗糙水平面内存在着2n个有理想边界的匀强电场区,水平向右的电场和竖直向上的电场相互间隔,每一电场区域场强的大小均为E,且 E= ,电场宽度均为d,水平面粗糙摩擦系数为μ,一个质量为m,带正电的、电荷量为q的物体(看作质点),从第一个向右的电场区域的边缘由静止进入电场,则物体从开始运动到离开第2n个电场区域的过程中,求:
,电场宽度均为d,水平面粗糙摩擦系数为μ,一个质量为m,带正电的、电荷量为q的物体(看作质点),从第一个向右的电场区域的边缘由静止进入电场,则物体从开始运动到离开第2n个电场区域的过程中,求:
(1)电场力对物体所做的总功? 摩擦力对物体所做的总功?
(2)物体在第2n个电场(竖直向上的)区域中所经历的时间?
(3)物体在所有水平向右的电场区域中所经历的总时间?
(1)nmgd ;-nμmgd(2) (3)
(3)
解析试题分析:(1)电场力对物体所做的总功 W电=nEqd=nmgd.
摩擦力对物体所做的总功Wf=-nμmgd.
(2)根据动能定理得,W电?Wf= mv2, 即 nmgd-nμmgd=
mv2, 即 nmgd-nμmgd= mv2
mv2
解得 .
.
物体在第2n个电场中,电场力竖直向上等于竖直向下的重力,所以物体匀速运动  .
.
(3)若将物体在水平向右的加速电场中的运动连起来,物体的运动可以看作初速为0的匀加速直线运动, .
.
解得 .
.
考点:牛顿定律及动能定理。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 =_________,如果地面的动摩擦因数变小,两者一起沿水平地面作匀加速运动,则
=_________,如果地面的动摩擦因数变小,两者一起沿水平地面作匀加速运动,则
 =
= ,绳长l=2m,绳的悬挂点O距水面的高度为H=3m。不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深。(取重力加速度
,绳长l=2m,绳的悬挂点O距水面的高度为H=3m。不考虑空气阻力和绳的质量,浮台露出水面的高度不计,水足够深。(取重力加速度 ,
, ,
, )
)
 ,平均阻力
,平均阻力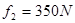 ,求选手落入水中的深度
,求选手落入水中的深度 。
。
 ,为使小车恰好能通过圆形轨道的最高点D,则它在P点沿斜面向下的初速度v0。
,为使小车恰好能通过圆形轨道的最高点D,则它在P点沿斜面向下的初速度v0。



 =1.4。求:
=1.4。求: