题目内容
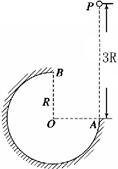
如图，在竖直平面内有一个半径为R的光滑圆弧轨道，半径OA竖直、OC水平，一个质量为m的小球自C点的正上方P点由静止开始自由下落，从C点沿切线进入轨道，小球沿轨道到达最高点A时恰好对轨道没有压力。重力加速度为
，不计一切摩擦和阻力。求：
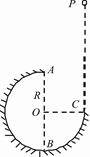
（1）小球到达轨道最高点A时的速度大小；
（2）小球到达轨道最低点B时对轨道的压力大小。
（1）
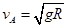（2）
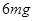
解析试题分析：（1） 设小球在A点速度大小为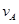
，小球到达A点由重力提供向心力得：
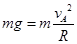①………………………………………………2分
可得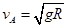： ……………………………………………………2分
设小球在B点速度大小为
，从B到A由机械能守恒得：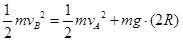
②………………………………………2分
在B点由牛顿第二定律可得：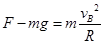 
③ ……………… 2分
由①②③计算可得：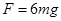 
……………………………………………1分
在B点，小球对轨道的压力为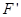
，由牛顿第三定律可得：
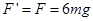④………………………………………1分
考点：考查了机械能守恒定律，圆周运动，牛顿运动定律
练习册系列答案
相关题目
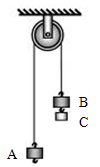
如右图所示，小车上有一直立木板，木板上方有一槽，槽内固定一定滑轮，跨过定滑轮的轻绳一端系一重球，另一端系在轻质弹簧测力计上，弹簧测力计固定在小车上，开始时小车处于静止状态，轻绳竖直且重球恰好紧挨直立木板，假设重球和小车始终保持相对静止，则下列说法正确的是( )
| A．若小车匀加速向右运动，弹簧测力计读数及小车对地面压力均不变 |
| B．若小车匀加速向左运动，弹簧测力计读数及小车对地面压力均不变 |
| C．若小车匀加速向右运动，弹簧测力计读数变大，小车对地面压力变小 |
| D．若小车匀加速向左运动，弹簧测力计读数变大，小车对地面压力不变 |
=
，绳长l=2m，绳的悬挂点O距水面的高度为H=3m。不考虑空气阻力和绳的质量，浮台露出水面的高度不计，水足够深。（取重力加速度
，
，
）
，平均阻力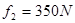
，求选手落入水中的深度
。
的速度向B点运动，如图所示， AB=4R，物块沿圆形轨道通过最高点C后做平抛运动，最后恰好落回出发点A。（ g取10 m/s2），求： 
内存在水平向右的匀强电场，场强大小E=10N／c，在y≥0的区域内还存在垂直于坐标平面向里的匀强磁场，磁感应强度大小B=0.5T一带电量
、质量
的小球由长
的细线悬挂于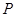
点小球可视为质点，现将小球拉至水平位置A无初速释放，小球运动到悬点
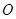时，悬线突然断裂，此后小球又恰好能通过
)，求：
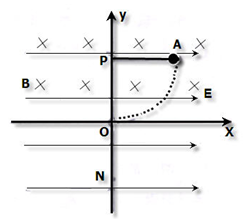
间的距离。