题目内容
5．
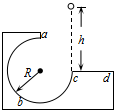如图，有缺口的方形木块固定在水平桌面上，abc为足够光滑、半径是R的$\frac{3}{4}$圆形轨道，ɑ为轨道最高点，cd面水平且有一定长度，今将一小球在c点的正上方高为h处由静止释放，其自由下落到c处切入轨道内运动，则以下论断正确的是（ ）| A． | 只要h大于R，释放后小球就能通过a点 | |
| B． | 调节h，可以使小球通过a点做自由落体运动 | |
| C． | 无论怎样改变h，都不可能使小球通过a点后落回轨道内 | |
| D． | 只要改变h，就能使小球通过a点后，既可以落回轨道内又可以落到cd平面上 |
分析 根据牛顿第二定律分析小球的加速度与质量的关系．若小球恰能通过a点，其条件是小球的重力提供向心力，根据牛顿第二定律可解得小球此时的速度，用平抛运动的规律：水平方向的匀速直线运动，竖直方向的自由落体运动规律求出水平距离，由机械能守恒定律可求得h，分析小球能否通过a点后落回轨道内．
解答 解：A、小球恰能通过a点的条件是小球的重力提供向心力，根据牛顿第二定律：mg=m$\frac{{v}^{2}}{R}$，解得：v=$\sqrt{gR}$，根据动能定理：mg（h-R）=$\frac{1}{2}$mv2，得：h=1.5R
可知只有满足h≥1.5R，释放后小球才能通过a点，故A错误；
BCD、小球离开a点时做平抛运动，用平抛运动的规律，水平方向的匀速直线运动：x=vt，竖直方向的自由落体运动：R=$\frac{1}{2}$gt2，解得：x=$\sqrt{2}$R＞R，故无论怎样改变h的大小，都不可能使小球通过a点后落回轨道内，小球将通过a点不可能到达d点．只要改变h的大小，就能改变小球到达a点的速度，就有可能使小球通过a点后，落在de之间或之外．故BD错误，C正确．
故选：C．
点评 本题实质是临界问题，要充分挖掘临界条件，要理解平抛运动的规律：水平方向的匀速直线运动，竖直方向的自由落体运动．
练习册系列答案
相关题目
13．
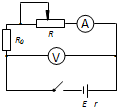如图所示，定值电阻阻值为R0，电池电动势为E，内阻为r=R0，滑动变阻器最多电阻R=2R0，不考虑电表内阻影响，则下列判定正确的是（ ）
如图所示，定值电阻阻值为R0，电池电动势为E，内阻为r=R0，滑动变阻器最多电阻R=2R0，不考虑电表内阻影响，则下列判定正确的是（ ）| A． | 改变R，伏特表最大示数为$\frac{3}{4}$E | |
| B． | 改变R，安培表最大示数为$\frac{E}{4{R}_{0}}$ | |
| C． | R=0时，R0上获得最大功率，且最大功率为$\frac{{E}^{2}}{4{R}_{0}}$ | |
| D． | R=2R0时，电源输出功率最大，效率最高 |
20．
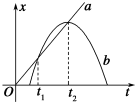如图所示，a、b分别为甲、乙两物体在同一直线上运动时的位移与时间的关系图象，其中a为过原点的倾斜直线，b为开口向下的抛物线．下列说法正确的是（ ）
如图所示，a、b分别为甲、乙两物体在同一直线上运动时的位移与时间的关系图象，其中a为过原点的倾斜直线，b为开口向下的抛物线．下列说法正确的是（ ）| A． | 物体乙始终沿正方向运动 | |
| B． | t1时刻甲、乙两物体的位移相等、速度相等 | |
| C． | t1到t2时间内两物体的平均速度相同 | |
| D． | 0～t2时间内物体乙的平均速度大于物体甲的平均速度 |
10．
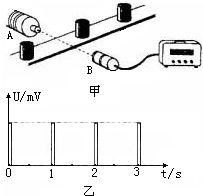利用光敏电阻制作的光传感器，记录了传递带上工件的输 送情况．如图甲所示为某工厂成品包装车间的光传感记录器，光传感器B能接收到发光元件A发出的光．每当工件挡住A发出的光时，光传感器就输出一个电信号，并在屏幕上显示出电信号与时间的关系，如图乙所示．若传送带始终匀速运动，每两个工件间的距离为0.2m，则下述说法正确的是（ ）
利用光敏电阻制作的光传感器，记录了传递带上工件的输 送情况．如图甲所示为某工厂成品包装车间的光传感记录器，光传感器B能接收到发光元件A发出的光．每当工件挡住A发出的光时，光传感器就输出一个电信号，并在屏幕上显示出电信号与时间的关系，如图乙所示．若传送带始终匀速运动，每两个工件间的距离为0.2m，则下述说法正确的是（ ）| A． | 传送带运动的速度是0.1 m/s | B． | 传送带运动的速度是0.2 m/s | ||
| C． | 该传送带每小时输送3600个工件 | D． | 该传送带每小时输送7200个工件 |
如图所示，两轻绳系一个质量为m的小球，两绳的另一端分别固定于轴的A、B两处，上面的绳长l=2m，两绳都拉直时与轴夹角分别为30°和45°，则小球随轴转动的角速度ω满足什么条件时，两绳始终被拉直．（g取10m/s2，结果保留两位有效数字）
通电螺线管的横截面如图所示，放在通电螺线管内的小磁针可以绕其中心自由转动，最后小磁针处于静止状态．试在图上导线的横截面积0内标出电流方向．