题目内容
1.跳伞运动员从120m高空离开直升飞机开始由静止下降,最初未打开伞,以加速度10m/s2下落一段距离后才打开伞,打开伞后以2m/s2的加速度匀减速下降,到达地面时速度恰好为0,求跳伞运动员打开伞时离地高度.分析 根据速度位移公式,结合匀加速直线运动和匀减速直线运动的位移之和等于120m求出匀加速直线运动的末速度,根据速度位移公式求出打开伞时离地的高度.
解答 解:设匀加速直线运动的末速度为v,根据速度位移公式有:$\frac{{v}^{2}}{2{a}_{1}}+\frac{{v}^{2}}{2{a}_{2}}=H$,
即:$\frac{{v}^{2}}{20}+\frac{{v}^{2}}{4}=120$,
解得:v=20m/s,
则跳伞运动员打开伞时离地的高度为:h=$\frac{{v}^{2}}{2{a}_{2}}=\frac{400}{4}m=100m$.
答:跳伞运动员打开伞时离地高度为100m.
点评 解决本题的关键知道运动员先做匀加速直线运动,然后做匀减速直线运动,抓住位移之和求出匀加速直线运动的末速度是解决本题的突破口.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.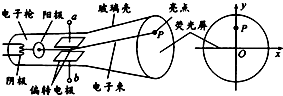 如图所示为阴极射线管的结构示意图,从阴极脱离出来的电子经阴极和阳极之间的加速电场加速后通过阳极上的小孔.然后在偏转电极间电场作用下发生偏转并最终打在荧光屏上形成亮点P.关于阴极射线管的工作原理,下列说法正确的是
如图所示为阴极射线管的结构示意图,从阴极脱离出来的电子经阴极和阳极之间的加速电场加速后通过阳极上的小孔.然后在偏转电极间电场作用下发生偏转并最终打在荧光屏上形成亮点P.关于阴极射线管的工作原理,下列说法正确的是
( )
 如图所示为阴极射线管的结构示意图,从阴极脱离出来的电子经阴极和阳极之间的加速电场加速后通过阳极上的小孔.然后在偏转电极间电场作用下发生偏转并最终打在荧光屏上形成亮点P.关于阴极射线管的工作原理,下列说法正确的是
如图所示为阴极射线管的结构示意图,从阴极脱离出来的电子经阴极和阳极之间的加速电场加速后通过阳极上的小孔.然后在偏转电极间电场作用下发生偏转并最终打在荧光屏上形成亮点P.关于阴极射线管的工作原理,下列说法正确的是( )
| A. | 当偏转电极的电势φa<φb时,电子流将可能沿图示径迹运动并在荧光屏上形成亮点P | |
| B. | 若只增加阴极和阳极间的加速电压,亮点P将沿y轴远离荧光屏中心O | |
| C. | 若只减小偏转电极间的电压,亮点P将沿y轴靠近荧光屏中心O | |
| D. | 若只增加偏转电极间的电压,电子从阴极出发运动到荧光屏的时间将增长 |
9.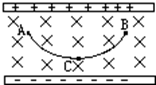 设空间存在竖直向下的匀强电场和垂直纸面向里的匀强磁场,如图所示,已知一离子在电场力和洛仑兹力的作用下,从静止开始自A点沿曲线ACB运动,到达B点时速度为零,C点是运动的最低点,忽略重力,以下说法中正确的是( )
设空间存在竖直向下的匀强电场和垂直纸面向里的匀强磁场,如图所示,已知一离子在电场力和洛仑兹力的作用下,从静止开始自A点沿曲线ACB运动,到达B点时速度为零,C点是运动的最低点,忽略重力,以下说法中正确的是( )
 设空间存在竖直向下的匀强电场和垂直纸面向里的匀强磁场,如图所示,已知一离子在电场力和洛仑兹力的作用下,从静止开始自A点沿曲线ACB运动,到达B点时速度为零,C点是运动的最低点,忽略重力,以下说法中正确的是( )
设空间存在竖直向下的匀强电场和垂直纸面向里的匀强磁场,如图所示,已知一离子在电场力和洛仑兹力的作用下,从静止开始自A点沿曲线ACB运动,到达B点时速度为零,C点是运动的最低点,忽略重力,以下说法中正确的是( )| A. | 这离子可能带负电荷 | |
| B. | A点和B点位于同一高度 | |
| C. | 离子在C点时速度最大 | |
| D. | 离子到达B点后,将沿原曲线返回A点 |
13.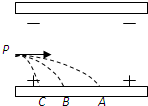 如图所示,有三个质量相等分别带正电、负电和不带电的小球,从平行板电场中的P点以相同的初速度垂直于电场方向进入电场,它们分别落到A、B、C三点,则可以断定( )
如图所示,有三个质量相等分别带正电、负电和不带电的小球,从平行板电场中的P点以相同的初速度垂直于电场方向进入电场,它们分别落到A、B、C三点,则可以断定( )
 如图所示,有三个质量相等分别带正电、负电和不带电的小球,从平行板电场中的P点以相同的初速度垂直于电场方向进入电场,它们分别落到A、B、C三点,则可以断定( )
如图所示,有三个质量相等分别带正电、负电和不带电的小球,从平行板电场中的P点以相同的初速度垂直于电场方向进入电场,它们分别落到A、B、C三点,则可以断定( )| A. | 落到A点的小球带正电,落到B点的小球不带电,落到C点的小球带负电 | |
| B. | 三小球在电场中运动时间相等 | |
| C. | 三小球到达正极板的动能关系:EKA>EKB>EKC | |
| D. | 三小球在电场中运动的加速度关系:aA>aB>aC |
11.以v0=12m/s的速度匀速行驶的汽车,突然刹车做匀减速直线运动,刹车过程汽车加速度大小为6m/s2,则刹车后( )
| A. | 2 s末停止运动 | B. | 3 s内的位移是9 m | ||
| C. | 1 s末速度的大小是18 m/s | D. | 3 s末速度的大小是6 m/s |
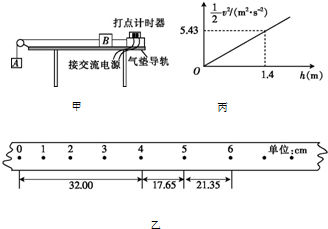
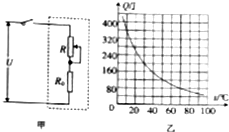 图甲是一种家用电熨斗的电路原理图(额定电压为220V),虚线框内为加热电路,R0是定值电阻,R是可变电阻.当该电熨斗所接电压为其额定电压时,该电熨斗的最低耗电功率为100W,最高耗电功率为500W.
图甲是一种家用电熨斗的电路原理图(额定电压为220V),虚线框内为加热电路,R0是定值电阻,R是可变电阻.当该电熨斗所接电压为其额定电压时,该电熨斗的最低耗电功率为100W,最高耗电功率为500W.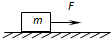 如图所示,质量m=2kg的物体原静止在光滑的水平地面上,一个沿水平方向的恒力F=12N作用在这个物体上,(g取10m/s2)求:
如图所示,质量m=2kg的物体原静止在光滑的水平地面上,一个沿水平方向的恒力F=12N作用在这个物体上,(g取10m/s2)求: