题目内容
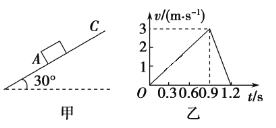
【题目】如图甲,两条光滑平行金属导轨固定,所在平面与水平面夹角为θ,导轨电阻忽略不计。虚线ab、cd均与导轨垂直,在ab与cd之间的区域存在垂直于导轨所在平面的匀强磁场。将两根相同的导体棒PQ、MN,先后自导轨上同一位置由静止释放,两者始终与导轨垂直且接触良好。已知PQ进入磁场开始计时,到MN离开磁场区域为止,流过PQ的电流随时间变化的图像如图乙所示。已知数据有轨道倾角θ=30°,磁感应强度为B=2T,图像中电流值I0=1A,两导体棒电阻均为R=2Ω,轨道宽度为d=0.5m,重力加速度取g=10m/s2。

(1)分析在t2时刻,PQ棒是否在磁场ab和cd之间?直接给出结论即可。
(2)求在t2时刻,导体棒MN的速度v,以及导体棒的质量m。
(3)若流过PQ的电流随时间变化的图像如图丙所示,已知![]() 到
到 ![]() 的时间间隔为
的时间间隔为![]() =0.2s,此过程通过导体的电荷量q=1C,求这段时间内的最大加速度a为多大?
=0.2s,此过程通过导体的电荷量q=1C,求这段时间内的最大加速度a为多大?
【答案】(1)否(2)4m/s,0.2kg(3)5m/s2
【解析】
(1)由图乙可知,0-t1时间内导体棒PQ中的电流恒定为I0,可知导体棒PQ在磁场中匀速运动; t1- t2时间内导体棒PQ已经滑出磁场区域,导体棒MN尚未进入磁场;t2时刻后,导体棒PQ中的电流反向且恒定为- I0,可知此时导体棒MN刚进入磁场,且PQ已经滑出磁场区域,即在t2时刻,PQ棒不在磁场ab和cd之间;
(2)由![]()
由于![]()
可得:![]()
对导体棒MN:![]()
解得m=0.2kg
(3) 设沿斜面向下为正方向,设![]() 时刻MN棒的速度为v1,由动量定理:
时刻MN棒的速度为v1,由动量定理:![]()
且![]()
解得:v1=8m/s
由牛顿第二定律:![]()
![]()
解得a=5m/s2
即此过程中最大加速度为5m/s2

练习册系列答案
相关题目