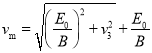题目内容
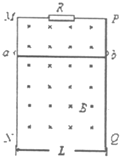
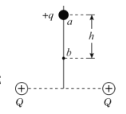
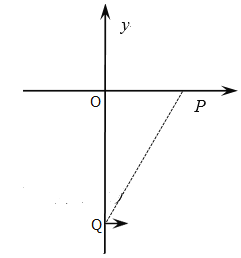
【题目】如图，xOy平面处于匀强磁场中，磁感应强度大小为B，方向垂直纸面向外。点P（
，0）处有一粒子源，向各个方向发射速率不同、质量为m、电荷量为－q的带电粒子。粒子1以某速率v1发射，先后经过第一、二、三象限后，恰好沿x轴正向通过点Q（0，－L）。不计粒子的重力。
(1)求粒子1的速率v1和第一次从P到Q的时间t1；
(2)若只撤去第一象限的磁场，另在第一象限加y轴正向的匀强电场，粒子2以某速率v2发射，先后经过第一、二、三象限后，也以速率v1沿x轴正向通过点Q，求匀强电场的电场强度大小E以及粒子2的发射速率v2；
(3)若在xOy平面内加上沿y轴负向的匀强电场，场强大小为 E0，粒子3以速率 v3 沿 y 轴正向发射，粒子将做复杂的曲线运动，求粒子3在运动过程中的最大速率 vm。某同学查阅资料后，得到一种处理相关问题的思路：带电粒子在正交的匀强磁场和匀强电场中运动，若所受洛伦兹力与电场力不平衡而做复杂的曲线运动时，根据运动的独立性和矢量性，可将带电粒子的初速度进行分解，将带电粒子的运动等效为沿某方向的匀速直线运动和沿某一时针方向的匀速圆周运动的合运动。本题中可将带电粒子的运动等效为沿x轴负方向的匀速直线运动和沿某一时针方向的匀速圆周运动的合运动。请尝试用该思路求解粒子3的最大速率vm。
【答案】(1)
，
；(2)
，
；(3)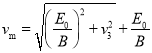
【解析】
(1)粒子1在第一、二、三象限做圆周运动，轨迹如图：
设半径为
，由几何知识得
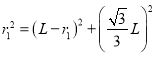
可得
由向心力公式，根据牛顿第二定律
可得
设粒子做圆周运动的周期为
由几何知识可知
粒子第一次从P到Q的时间
(2)粒子2在二、三象限的运动与粒子1完全相同，粒子2在第一象限做类斜抛运动，并且垂直经E过y轴，可以逆向思考，由牛顿第二定律得
x轴方向
y轴方向
可得
根据
可得
(3)根据提示，可将粒子的初速度分解，如图：
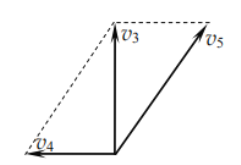
根据平衡条件
可得
根据运动的合成，可知
粒子的运动可视为水平向左的速率为
的匀速直线运动和初速度为
的逆时针的圆周运动的合运动，所以粒子的最大速率为
可得
