题目内容
20.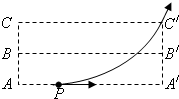 如图所示,空间的虚线框内有匀强电场,AA′、BB′、CC′是该电场的三个等势面.相邻等势面间的距离为0.5cm,其中BB′为零势面,一个质量为m、带电量为+q的粒子沿AA′方向以初速度2m/s自图中的P点进入电场,刚好从C′点离开电场.已知PA′=2cm,粒子的比荷为0.1,粒子的重力忽略不计.求:
如图所示,空间的虚线框内有匀强电场,AA′、BB′、CC′是该电场的三个等势面.相邻等势面间的距离为0.5cm,其中BB′为零势面,一个质量为m、带电量为+q的粒子沿AA′方向以初速度2m/s自图中的P点进入电场,刚好从C′点离开电场.已知PA′=2cm,粒子的比荷为0.1,粒子的重力忽略不计.求:(1)匀强电场强度的大小和方向;
(2)等势面AA′、BB′、CC′的电势;
(3)若粒子在P点的动能为Ek,则在P、C′点时的电势能(请用Ek表示).
分析 (1)BB′为零势面,知匀强电场的方向竖直向上,带电粒子做类平抛运动,根据水平方向上做匀速直线运动,竖直方向上做初速度为零的匀加速直线运动,根据分位移公式和牛顿第二定律求场强的大小.
(2)根据U=Ed求解出相邻等势面间的电势差,再求电势.
(3)求出末速度与初速度的关系,从而得出末动能和初动能的关系,根据动能定理和电场力做功与电势能的关系得出C′点的电势能.
解答 解:(1)带电粒子做类平抛运动,水平方向上做匀速直线运动,竖直方向上做初速度为零的匀加速直线运动,有:
x=v0t
y=$\frac{1}{2}a{t}^{2}$
又 a=$\frac{qE}{m}$
解得 E=$\frac{2m{v}_{0}^{2}y}{q{x}^{2}}$=$\frac{2×{2}^{2}×0.01}{0.1×0.0{2}^{2}}$=4000N/C
场强方向竖直向上.
(2)相邻等势面间的电势差 U=Ed=4000×0.005V=20V
根据顺着电场线方向电势降低,可知,等势面AA′、BB′、CC′的电势依次降低,则等势面AA′、BB′、CC′的电势分别为:20V、0、-20V.
(3)从等势面AA′到CC′有:
水平方向有:x=v0t=2cm
竖直方向有:y=$\frac{{v}_{y}}{2}t$=1cm
解得 vy=v0
粒子的初速度为 Ek=$\frac{1}{2}m{v}_{0}^{2}$
粒子到达C′点时的动能EK′=$\frac{1}{2}$mv2=$\frac{1}{2}m$(${v}_{0}^{2}$+${v}_{y}^{2}$)=2EK.
根据动能定理得:qUPC′=2EK-Ek=Ek
则从P到BB′,有:qUPBB′=q•$\frac{1}{2}$UPC′=0.5Ek
根据功能关系可得,P、C′点时的电势能分别为:0.5Ek,-0.5Ek.
答:
(1)匀强电场强度的大小为4000N/C,场强方向竖直向上.
(2)等势面AA′、BB′、CC′的电势分别为20V、0、-20V;
(3)若粒子在P点的动能为Ek,则在P、C′点时的电势能分别为0.5Ek,-0.5Ek.
点评 解决本题的关键知道粒子做类平抛运动,知道水平方向上和竖直方向上的运动规律,以及掌握动能定理和电场力做功与电势能的关系.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案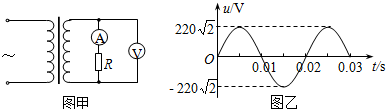
| A. | 电流表示数为2A | |
| B. | 电流表示数为2$\sqrt{2}$A | |
| C. | 原、副线圈的匝数之比为1:2 | |
| D. | 原、副线圈中交变电压的频率均为100Hz |
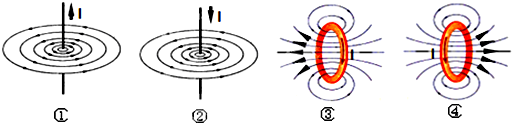
| A. | ①③ | B. | ②③ | C. | ①④ | D. | ②④ |
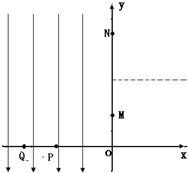 如图所示,xOy平面内,y轴左侧存在着沿y轴负方向的匀强电场,y轴右侧直线y=2a(图中虚线)上方存在着一个匀强磁场区域,磁场方向垂直xOy平面(图中未画出).一个质量为m、带电荷量为+q的粒子从坐标P(-2a,0)以速度v0沿x轴正方向开始运动.经过M(0,a)点进入y轴右侧,通过磁场区域后,从N点垂直经过y轴第二次进入电场时,电场反向场,强大小不变.不计粒子的重力,试求:
如图所示,xOy平面内,y轴左侧存在着沿y轴负方向的匀强电场,y轴右侧直线y=2a(图中虚线)上方存在着一个匀强磁场区域,磁场方向垂直xOy平面(图中未画出).一个质量为m、带电荷量为+q的粒子从坐标P(-2a,0)以速度v0沿x轴正方向开始运动.经过M(0,a)点进入y轴右侧,通过磁场区域后,从N点垂直经过y轴第二次进入电场时,电场反向场,强大小不变.不计粒子的重力,试求: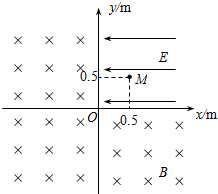 如图所示,在直角坐标系的第I象限分布着场强E=5×103V/m,方向水平向左的匀强电场,其余三象限分布着垂直纸面向里的匀强磁场.现从电场中M(0.5,0.5)点由静止释放一重力不计的带正电粒子,粒子的电荷量q=2×10-4C,质量m=1×10-8kg,该粒子第一次进入磁场后将垂直通过x轴.求:
如图所示,在直角坐标系的第I象限分布着场强E=5×103V/m,方向水平向左的匀强电场,其余三象限分布着垂直纸面向里的匀强磁场.现从电场中M(0.5,0.5)点由静止释放一重力不计的带正电粒子,粒子的电荷量q=2×10-4C,质量m=1×10-8kg,该粒子第一次进入磁场后将垂直通过x轴.求: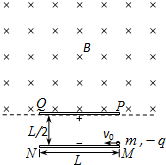 如图所示,MN、PQ是平行带电长金属板,板长为L,两板间距离为$\frac{L}{2}$,在PQ板的上方有垂直纸面向里的匀强磁场.一个电荷量为q、质量为m的带负电粒子以速度v0从负极板MN边缘M点沿平行于板的方向从右向左射入两板间,结果粒子恰好从正极板PQ左边缘Q点飞进磁场,然后又恰好从PQ板的右边缘P点飞进电场,直到飞出电场.不计粒子的重力,试求:
如图所示,MN、PQ是平行带电长金属板,板长为L,两板间距离为$\frac{L}{2}$,在PQ板的上方有垂直纸面向里的匀强磁场.一个电荷量为q、质量为m的带负电粒子以速度v0从负极板MN边缘M点沿平行于板的方向从右向左射入两板间,结果粒子恰好从正极板PQ左边缘Q点飞进磁场,然后又恰好从PQ板的右边缘P点飞进电场,直到飞出电场.不计粒子的重力,试求: