题目内容
15.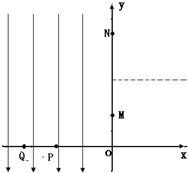 如图所示,xOy平面内,y轴左侧存在着沿y轴负方向的匀强电场,y轴右侧直线y=2a(图中虚线)上方存在着一个匀强磁场区域,磁场方向垂直xOy平面(图中未画出).一个质量为m、带电荷量为+q的粒子从坐标P(-2a,0)以速度v0沿x轴正方向开始运动.经过M(0,a)点进入y轴右侧,通过磁场区域后,从N点垂直经过y轴第二次进入电场时,电场反向场,强大小不变.不计粒子的重力,试求:
如图所示,xOy平面内,y轴左侧存在着沿y轴负方向的匀强电场,y轴右侧直线y=2a(图中虚线)上方存在着一个匀强磁场区域,磁场方向垂直xOy平面(图中未画出).一个质量为m、带电荷量为+q的粒子从坐标P(-2a,0)以速度v0沿x轴正方向开始运动.经过M(0,a)点进入y轴右侧,通过磁场区域后,从N点垂直经过y轴第二次进入电场时,电场反向场,强大小不变.不计粒子的重力,试求:(1)电场强度的大小;
(2)磁场区域磁感强度;
(3)粒子最后经过x轴的速度大小.
分析 (1)粒子在电场中做类平抛运动,应用类平抛运动规律可以求出电场强度;
(2)求出粒子进入磁场的速度,粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律可以求出磁感应强度;
(3)粒子再次进入电场后做类平抛运动,应用动能定理可以求出粒子的速度.
解答 解:(1)粒子在磁场中做类平抛运动,
x轴方向:v0t=2a,
y轴方向:$\frac{1}{2}•\frac{qE}{m}{t^2}=a$
解得:$E=\frac{mv_0^2}{2qa}$; (2)粒子过M点时速度:$v=\sqrt{2}{v_0}$,与y轴正方向成45°角,
(2)粒子过M点时速度:$v=\sqrt{2}{v_0}$,与y轴正方向成45°角,
过y轴后先作直线运动,然后圆周运动,如图所示:
则圆周运动半径:$r=\sqrt{2}a$,
由牛顿第二定律得:$qvB=m\frac{v^2}{r}$,
解得:$B=\frac{{m{v^{\;}}}}{qr}=\frac{{m\sqrt{2}{v_0}^{\;}}}{{q\sqrt{2}a}}=\frac{{m{v_0}^{\;}}}{qa}$;
(3)第二次进入电场,电场反向,粒子作类平抛运动经过Q点,
由动能定理得:qEyON=$\frac{1}{2}$mv′2-$\frac{1}{2}$mv2,
解得:v′=$\sqrt{5+\sqrt{2}}$v0;
答:(1)电场强度的大小为$\frac{m{v}_{0}^{2}}{2qa}$;
(2)磁场区域磁感强度为$\frac{m{v}_{0}}{qa}$;
(3)粒子最后经过x轴的速度大小为$\sqrt{5+\sqrt{2}}$v0.
点评 本题考查了粒子在电场与磁场中的运动,粒子在电场中做类平抛运动、在磁场中做匀速圆周运动,分析清楚粒子运动过程是正确解题的关键,应用类平抛运动规律、牛顿第二定律与动能定理可以解题.

 名校课堂系列答案
名校课堂系列答案| A. | 伽利略在斜面实验事实的基础上推理,提出了“力不是维持物体运动的原因” | |
| B. | 天文学家幵普勒对第谷观测的行星数据进行了多年研究,得出了万有引力定律 | |
| C. | 物理学家卡文迪许利用“卡文迪许扭秤”首先较准确的测定了静电力常量 | |
| D. | 楞次发现了电磁感应现象,并研究得出了判断感应电流方向的方法--楞次定律 |
 2011年9月29日晚21时16分,我国将首个目标飞行器天宫一号发射升空,它将在两年内分别与神舟八号、神舟九号、神舟十号飞船对接,从而建立我国第一个空间实验室.假如神舟八号与天宫一号对接前所处的轨道如图所示,下列说法正确的是( )
2011年9月29日晚21时16分,我国将首个目标飞行器天宫一号发射升空,它将在两年内分别与神舟八号、神舟九号、神舟十号飞船对接,从而建立我国第一个空间实验室.假如神舟八号与天宫一号对接前所处的轨道如图所示,下列说法正确的是( )| A. | 神舟八号的加速度比天宫一号的加速度大 | |
| B. | 神舟八号的运行速度比天宫一号的运行速度大 | |
| C. | 神舟八号的运行周期比天宫一号的运行周期长 | |
| D. | 神舟八号通过加速后变轨可实现与天宫一号对接 |
| A. | 气体自发的扩散运动总是沿着分子热运动的无序性增大的方向进行 | |
| B. | 满足能量守恒定律的过程都可以自发地进行 | |
| C. | 一定质量的理想气体,当温度不变时,压强增大,分子的密集程度也增大 | |
| D. | 通过有限的过程可以把一个物体冷却到绝对零度 |
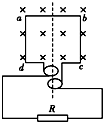 如图所示,线圈abcd的面积是0.05m2,共100匝,线圈电阻为r=1Ω,外接电阻R=5Ω,匀强磁场的磁感应强度为B=$\frac{1}{π}$T,当线圈以5r/s的转速匀速转动时( )
如图所示,线圈abcd的面积是0.05m2,共100匝,线圈电阻为r=1Ω,外接电阻R=5Ω,匀强磁场的磁感应强度为B=$\frac{1}{π}$T,当线圈以5r/s的转速匀速转动时( )| A. | 感应电动势的最大值为50V | |
| B. | 感应电流的有效值为8.33A | |
| C. | R两端电压的有效值为29.46V | |
| D. | 线圈从图示位置转过90°的过程中通过电阻R的电荷量为0.27C |
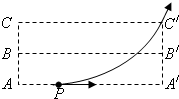 如图所示,空间的虚线框内有匀强电场,AA′、BB′、CC′是该电场的三个等势面.相邻等势面间的距离为0.5cm,其中BB′为零势面,一个质量为m、带电量为+q的粒子沿AA′方向以初速度2m/s自图中的P点进入电场,刚好从C′点离开电场.已知PA′=2cm,粒子的比荷为0.1,粒子的重力忽略不计.求:
如图所示,空间的虚线框内有匀强电场,AA′、BB′、CC′是该电场的三个等势面.相邻等势面间的距离为0.5cm,其中BB′为零势面,一个质量为m、带电量为+q的粒子沿AA′方向以初速度2m/s自图中的P点进入电场,刚好从C′点离开电场.已知PA′=2cm,粒子的比荷为0.1,粒子的重力忽略不计.求: